



Министерство образования и науки Российской Федерации
Новосибирский государственный технический университет
Лабораторная работа № 4
Вариант – 1
Факультет: АВТ Преподаватель:
Группа: АА-06 Шпилевая О.Я.
Студенты: Кузнецова И.В.
Веселков А.П.
Сагайдакова Т.А.
Дата выполнения: ………………………
Отметка о защите: ………………………
Новосибирск
2004
1. Цель работы
Изучение свойств системы с алгоритмом адаптации, синтезированным по методу старшей производной, исследование возможности понижения порядка адаптивного регулятора.
2. Исходные данные
|
N |
|
|
|
b |
|
|
|
1 |
-2 |
-3 |
-2 |
2 |
0 |
2 |
3. Ход работы
3.1 Определить элементы матриц ![]() ,
,![]() , по заданным показателям к качеству
процессов (табл.1).
, по заданным показателям к качеству
процессов (табл.1).
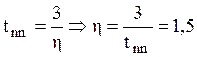
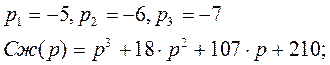
Получаем:
![]() =
=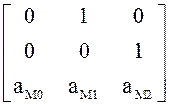 =
=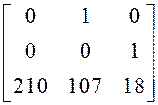 ,
, 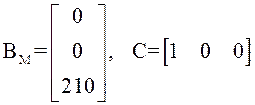
3.2. Определить элементы матриц ![]() ,
,![]() , учитывая что
, учитывая что ![]() .
.
![]()
![]() ;
; 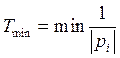 ;
; ![]() .
.
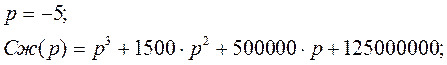
Получаем:
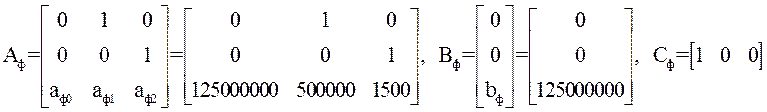
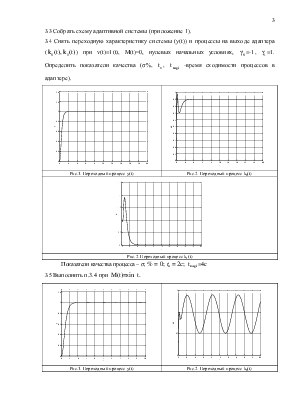
3.3 Собрать схему адаптивной системы (приложение 1).
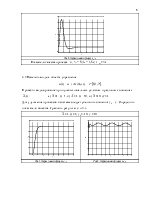
3.4 Снять переходную характеристику
системы (y(t)) и процессы на выходе адаптера (![]() ) при v(t)=1(t), M(t)=0, нулевых начальных условиях,
) при v(t)=1(t), M(t)=0, нулевых начальных условиях, ![]() =-1,
=-1, ![]() =1. Определить показатели качества (s%,
=1. Определить показатели качества (s%, ![]() ,
, ![]() -время сходимости процессов в адаптере).
-время сходимости процессов в адаптере).
|
|
|
|
Рис.1. Переходный процесс y(t) |
Рис.2. Переходный процесс k0(t) |
|
|
|
|
Рис.2. Переходный процесс k1(t) |
|
Показатели качества процесса – σ, % = 0;tn = 2c; ![]() =4c
=4c
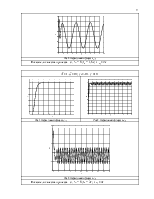
3.5 Выполнить п.3.4
при ![]()
|
|
|
|
Рис.1. Переходный процесс y(t) |
Рис.2. Переходный процесс k0(t) |
|
|
|
|
Рис.2. Переходный процесс k1(t) |
|
Показатели качества процесса – σ, % = 0;tn = 1,8c; ![]() =2c
=2c
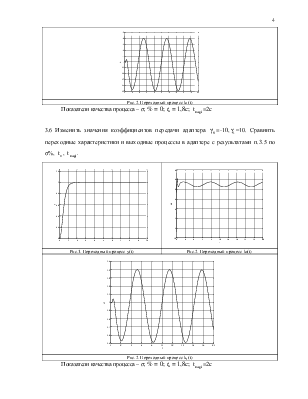
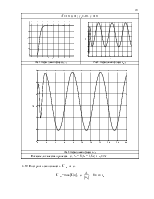
3.6 Изменить значения коэффициентов
передачи адаптера ![]() =-10,
=-10,![]() =10.
Сравнить переходные характеристики и выходные процессы в адаптере с
результатами п.3.5 по s%,
=10.
Сравнить переходные характеристики и выходные процессы в адаптере с
результатами п.3.5 по s%, ![]() ,
, ![]() .
.
|
|
|
|
Рис.1. Переходный процесс y(t) |
Рис.2. Переходный процесс k0(t) |
|
|
|
|
Рис.2. Переходный процесс k1(t) |
|
Показатели качества процесса – σ, % = 0;tn = 1,8c; ![]() =2c
=2c
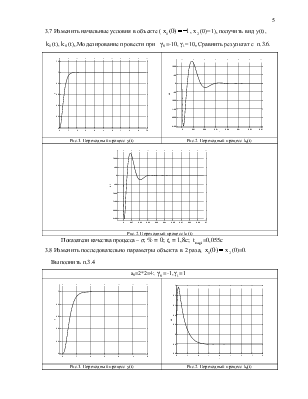
3.7 Изменить начальные условия в объекте (![]()
![]() (0)=1), получить вид y(t),
(0)=1), получить вид y(t), ![]() (t),
(t), ![]() (t),.Моделирование провести при
(t),.Моделирование провести при ![]() =-10,
=-10,![]() =10,.Сравнить результат с п.3.6.
=10,.Сравнить результат с п.3.6.
|
|
|
|
Рис.1. Переходный процесс y(t) |
Рис.2. Переходный процесс k0(t) |
|
|
|
|
Рис.2. Переходный процесс k1(t) |
|
Показатели качества процесса – σ, % = 0;tn = 1,8c; ![]() =0,055c
=0,055c
3.8 Изменить
последовательно параметры объекта в 2 раза, ![]()
![]() (0)=0. Выполнить п.3.4
(0)=0. Выполнить п.3.4
|
a0=2*2=4; |
|
|
|
|
|
Рис.1. Переходный процесс y(t) |
Рис.2. Переходный процесс k0(t) |
|
|
|
|
Рис.2. Переходный процесс k1(t) |
|
|
Показатели качества процесса – σ, % = 0;tn = 2c; |
|
|
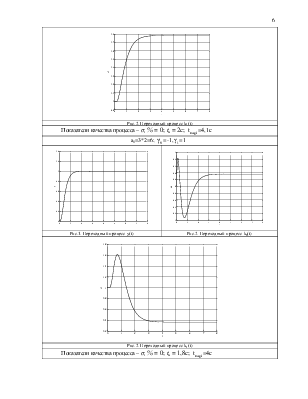
a1=3*2=6; |
|
|
|
|
|
Рис.1. Переходный процесс y(t) |
Рис.2. Переходный процесс k0(t) |
|
|
|
|
Рис.2. Переходный процесс k1(t) |
|
|
Показатели качества процесса – σ, % = 0;tn = 1,8c; |
|
|
a2=2*2=4; |
|
|
|
|
|
Рис.1. Переходный процесс y(t) |
Рис.2. Переходный процесс k0(t) |
|
|
|
|
Рис.2. Переходный процесс k1(t) |
|
|
Показатели качества процесса – σ, % = 0;tn = 1,8c; |
|
|
b=2*2=4; |
|
|
|
|
|
Рис.1. Переходный процесс y(t) |
Рис.2. Переходный процесс k0(t) |
|
|
|
|
Рис.2. Переходный процесс k1(t) |
|
|
Показатели качества процесса – σ, % = 0;tn = 1,8c; |
|
3.9 Изменить модель объекта управления
![]() ,
, ![]() .
.
Провести моделирование при нулевых начальных условиях и
различных значениях ![]() : а)
: а) ![]() =1,
=1, ![]() =1, б)
=1, б) ![]() =1,
=1, ![]() =10, в)
=10, в)
![]() =10,
=10, ![]() =1.
=1.
Для улучшения процессов в системе следует увеличить значения ![]() ,
, ![]() .
Определить показатели качества. Сравнить результат с п.3.4.
.
Определить показатели качества. Сравнить результат с п.3.4.
|
|
|
|
|
|
|
Рис.1. Переходный процесс y(t) |
Рис.2. Переходный процесс k0(t) |
|
|
|
|
Рис.2. Переходный процесс k1(t) |
|
|
Показатели качества процесса – σ, % = 0;tn = 1,8c; |
|
|
|
|
|
|
|
|
Рис.1. Переходный процесс y(t) |
Рис.2. Переходный процесс k0(t) |
|
|
|
|
Рис.2. Переходный процесс k1(t) |
|
|
Показатели качества процесса – σ, % = 0;tn = 2c; |
|
|
|
|
|
|
|
|
Рис.1. Переходный процесс y(t) |
Рис.2. Переходный процесс k0(t) |
|
|
|
|
Рис.2. Переходный процесс k1(t) |
|
|
Показатели качества процесса – σ, % = 0;tn = 1,8c; |
|
3.10 Построить
зависимость ![]() от
от ![]() ,
,
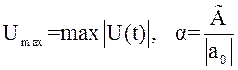 ,
, ![]()
где ![]() - время
наблюдения за процессом в системе. Амплитуду параметрических возмущений
выбирать из диапазона (0.1
- время
наблюдения за процессом в системе. Амплитуду параметрических возмущений
выбирать из диапазона (0.1![]() 100), например
(0.1,1.10,50,100),
100), например
(0.1,1.10,50,100), ![]() =1. Фиксировать значения
=1. Фиксировать значения ![]() , когда переходный процесс в системе
удовлетворяет заданными показателями качества. Значения
, когда переходный процесс в системе
удовлетворяет заданными показателями качества. Значения ![]() выбирать
от 1 до 200 в зависимости от амплитуды
выбирать
от 1 до 200 в зависимости от амплитуды ![]() .
.
а) ![]() =0,1,
=0,1, ![]() =1,
=1, ![]() =-1,
=-1, ![]() =1. σ, % = 0 ; tn = 2c
=1. σ, % = 0 ; tn = 2c
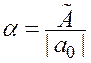 =
=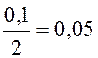 ;
umax = max |u(t)| = 104,6 (2,25).
;
umax = max |u(t)| = 104,6 (2,25).
б) ![]() =1,
=1, ![]() =1,
=1, ![]() =-1,
=-1, ![]() =1. σ, % = 0 ; tn = 2c
=1. σ, % = 0 ; tn = 2c
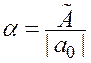 =
= ;
umax =
max |u(t)| = 104,6 (2,1).
;
umax =
max |u(t)| = 104,6 (2,1).
в) ![]() =10,
=10, ![]() =1,
=1, ![]() =-20,
=-20, ![]() =20. σ, % = 0 ; tn = 2c
=20. σ, % = 0 ; tn = 2c
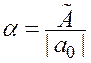 =
=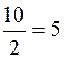 ;
umax =
max |u(t)| = 111,4 (6).
;
umax =
max |u(t)| = 111,4 (6).
г) ![]() =50,
=50, ![]() =1,
=1, ![]() =-100,
=-100, ![]() =100. σ, % = 0 ; tn = 2c
=100. σ, % = 0 ; tn = 2c
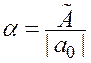 =
=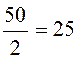 ;
umax =
max |u(t)| = 114,4 (26,93).
;
umax =
max |u(t)| = 114,4 (26,93).
д) ![]() =100,
=100, ![]() =1,
=1, ![]() =-100,
=-100, ![]() =100. σ, % = 0 ; tn = 2c
=100. σ, % = 0 ; tn = 2c
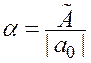 =
=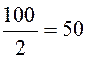 ;
umax =
max |u(t)| = 145,8 (50,9).
;
umax =
max |u(t)| = 145,8 (50,9).
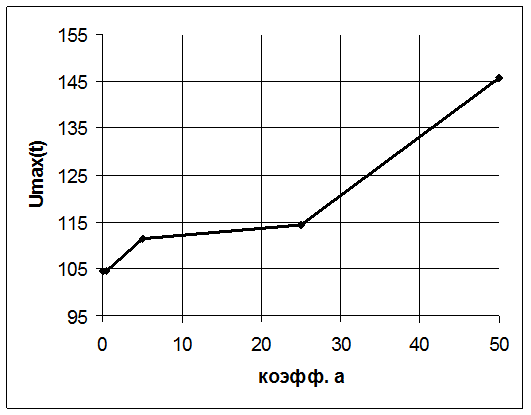
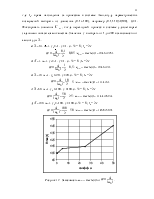
Рисунок 12 – Зависимость
umax =
max |u(t)| от 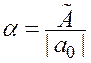 ,
,
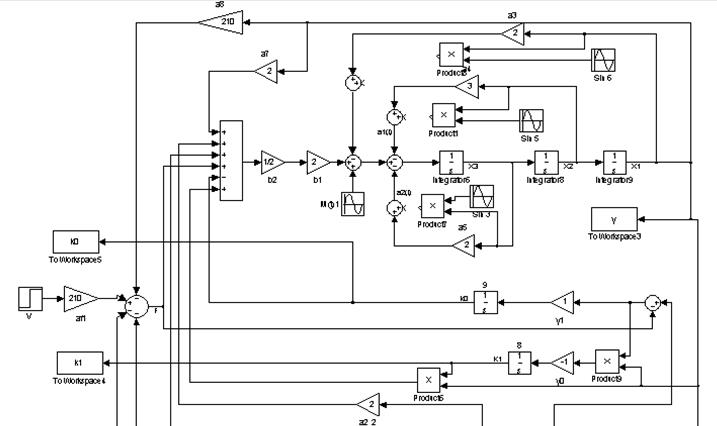
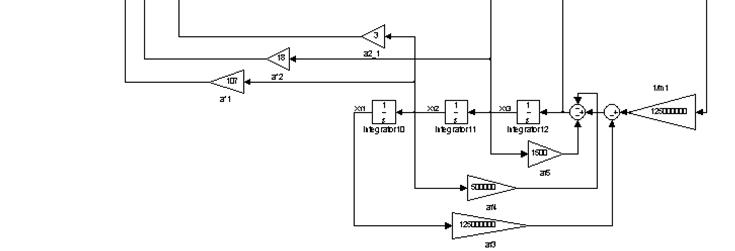
Приложение 1.
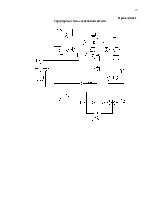
Структурная схема адаптивной системы
4. Выводы по работе
7.1 Если система неустойчива, то увеличивая параметр γ можно вернуть её в устойчивое состояние.
7.2 При ненулевых начальных условиях система теряет свое качество (по показателям переходного процесса σ, % и tn = 2c).
7.3 При введение параметрических возмущений в систему, наблюдаются следующие закономерности:
1. Увеличение
амплитуды ![]() “ухудшает” состояние системы.
“ухудшает” состояние системы.
2. Увеличение
частоты ![]() “улучшает”
состояние системы.
“улучшает”
состояние системы.
7.4 Изменение
коэффициента 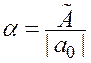 приводит к гармоническому изменению
управляющего воздействия (umax = max |u(t)|) на систему.
приводит к гармоническому изменению
управляющего воздействия (umax = max |u(t)|) на систему.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.