Вычислительная математика: Варианты и методические указания к индивидуальным заданиям

функции и  будут совпадать на рисунке в выбранном масштабе), то на одном рисунке следует построить график , а на другом ,   

1.4. Описание подпрограмм

Подпрограммы

N1YPLG  (A, B, KON, DT, L, RO, FI)

N1YPTH  (A, B, KON, DT, L, RO, TH)

N1YFLA  (A, B, KON, DT, L, RO, AL)

реализуют алгоритмы вычисления по рекуррентным формулам (см. раздел 1.2) реализаций базисных (Лежандра, Чебышева первого рода, Лагерра) и соответствующих весовых функций.

Входные параметры подпрограмм:

А – нижний предел а интервала аппроксимации;

В – верхний предел  интервала аппроксимации;

KON – количество дискретных значений функций на интервале аппроксимации;

DT – шаг дискретизации ;

L – число  учитываемых членов ряда Фурье.

Выходные параметры подпрограмм:

RO(K) – массив реализации весовой функции  для соответствующего базиса,

FI(IR,K) – массив реализаций полиномов Лежандра,  

TH(IR,K) – массив реализаций полиномов Чебышева первого рода,   

AL(IR,K) – массив реализаций функции Лагерра,  

Подпрограмма

N1YKF (KON, DT, L, F, F1, FR, RO, C)

реализует алгоритм вычисления коэффициентов Фурье.

Входные параметры подпрограммы:

KON, DT, L, RO(K) – см. описание предыдущих подпрограмм;

F(K) – массив реализации аппроксимируемой функции  

FR(IR,K) – массив реализаций базисных функций (Лежандра, Чебышева или Лагерра),  

Промежуточные параметры:

F1(K) – вспомогательный массив, необходимый для нормального функционирования подпрограммы,

Выходные параметры подпрограммы:

C(IR) – массив коэффициентов Фурье,

          В подпрограмме N1YKF осуществляется обращение к подпрограмме N1YIST, реализующей алгоритм вычисления определенного интеграла методом Симпсона.

Подпрограмма

N1YIST  (DT, U, NU, F)

реализует алгоритм вычисления определенного интеграла по квадратурной формуле парабол (формуле Симпсона).

          Входные параметры подпрограммы:

DT – шаг дискретизации ;

U(K) – массив реализации подынтегральной функции, K = 1, NU;

NU – количество дискретных значений подынтегральной функции на интервале интегрирования. 

        Выходные параметры подпрограммы:

F – значение вычисленного интеграла.

        В подпрограмме

N1YWST  (KON, L, C, FR, FF)

вычисляется массив реализации оценки аппроксимируемой функции.

        Входные параметры подпрограммы:

KON, L, C(IR), FR(IR,K) – см. описание предыдущих подпрограмм.

        Выходные параметры подпрограммы:

FF(K) – массив реализации оценки  аппроксимируемой функции  

        В подпрограмме

N1YTPG  (A, B, KON, DT, L, GC, CS)

вычисляются массивы реализаций четных и нечетных гармоник тригонометрических функций.

          Входные параметры подпрограммы:

A, B, KON, DT, L – см. описание предыдущих подпрограмм.

          Выходные параметры подпрограммы:

GC(IR,K) – массив реализаций четных гармоник тригонометрических функций,  

GS(IR,K) - массив реализаций нечетных гармоник тригонометрических функций,  

Подпрограмма

N1YKFG  (A, B, KON, F, F1, DT, L, AG, BG)

реализует алгоритм вычисления коэффициентов гармонического ряда Фурье.

          Входные параметры подпрограммы:

A, B, KON, DT, L – см. описание предыдущих подпрограмм;

F(K) – массив реализации аппроксимируемой функции

          Промежуточные параметры:

F1(K) – вспомогательный массив, необходимый для нормального функционирования подпрограммы,

          Выходные параметры подпрограммы:

AG(IR) – массив коэффициентов Фурье при четных гармониках,

BG(IR) – массив коэффициентов Фурье при нечетных гармониках,

          В подпрограмме N1YKFG осуществляется обращение к подпрограмме N1YIST, описание которой приведено выше.

          В подпрограмме

N1YWFG  (KON, L, AG, BG, GC, GS, FF)

вычисляется массив реализации оценки аппроксимируемой функции гармоническим рядом Фурье.

          Входные параметры подпрограммы:

KON, L, AG(IR), BG(IR), GC(IR,K), GS(IR,K) – см. описание предыдущих подпрограмм.

          Выходные параметры подпрограммы:

FF(K) – массив реализации оценки  аппроксимируемой функции        

          В подпрограмме

N1YEEE  (X, X1, N, E, EM, ES, EP, EMO, ESO, EPO)

вычисляются оценки погрешностей  между истинной функцией и ее оценкой.

          Входные параметры подпрограммы:

X(K) – массив реализации истинной функции  

X1(K) – массив реализации оценки  функции  

N – количество дискретных значений функций  и  на сравниваемом интервале.

          Выходные параметры подпрограммы:

E(K) – массив реализации погрешности  

EM – максимальная оценка погрешности

ES – среднеквадратичная оценка погрешности

EP – оценка смещенности (мат. ожидания)

EMO – относительная максимальная оценка погрешности

ESO – относительная среднеквадратичная оценка погрешность

EPO – оценка относительной смещенности (мат. ожидания)

2. РЕШЕНИЕ  ДИФФЕРЕНЦИАЛЬНОГО  УРАВНЕНИЯ

2.1. Постановка задачи

  На интервале  решить дифференциальное уравнение

      

            

с шагом дискретизации методом Адамса четвертого порядка точности с прогнозом и коррекцией решения. Необходимое для запуска численной процедуры Адамса количество точек решения вычислить методом Рунге-Кутта четвертого порядка точности.

  Определить на  погрешности решения дифференциального уравнения, для чего необходимо сравнить полученное решение  с точным , , вычисленным аналитически, которое для уравнение второго порядка с правой частью  имеет вид

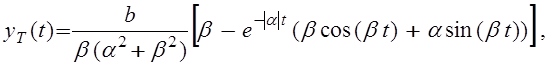
где  и  - вещественная и мнимая части корней характеристического уравнения

        

  Проанализировать влияние шага  решения дифференциального уравнения на точность решения, для чего необходимо изменить параметр  от  до c шагом

  Оценить методическую погрешность решения дифференциального уравнения по правилу Рунге, задавшись одним из используемых при численном решении значением параметра Dt. Сравнить оценку, вычисленную по правилу Рунге, с полученной при решении дифференциального уравнения методом Адамса.

Таблица  2.1

Варианты задания

№ п/п
1	10,0	0,0	10,0	[0; 160]	0,5	2,5	0,5
2	10,0	0,1	10,0	[0; 160]	0,5	2,5	0,5
3	10,0	0,2	10,0	[0; 160]	0,5	2,5	0,5
4	10,0	0,3	10,0	[0; 150]	0,5	2,5	0,5
5	10,0	0,4	10,0	[0; 140]	0,5	2,5	0,5
6	10,0	0,5	10,0	[0; 130]	0,5	2,5	0,5
7	10,0	0,6	10,0	[0; 120]	0,5	2,5	0,5
8	10,0	0,7	10,0	[0; 110]	0,5	2,5	0,5
9	10,0	0,9	10,0	[0; 100]	0,5	2,5	0,5
10	5,0	0,3	5,0	[0;   80]	0,2	1,0	0,2
11	5,0	0,5	5,0	[0;   70]	0,2	1,0	0,2
12	5,0	0,6	5,0	[0;   65]	0,2	1,0	0,2
13	5,0	0,7	5,0	[0;   60]	0,2	1,0	0,2
14	5,0	0,9	5,0	[0;   50]	0,2	1,0	0,2
15	2,0	0,0	2,0	[0;   32]	0,1	0,5	0,1
16	2,0	0,1	2,0	[0;   32]	0,1	0,5	0,1
17	2,0	0,2	2,0	[0;   32]	0,1	0,5	0,1
18	2,0	0,6	2,0	[0;   24]	0,1	0,5	0,1
19	2,0	0,8	2,0	[0;   20]	0,1	0,5	0,1
20	1,0	0,0	1,0	[0;   14]	0,05	0,09	0,01
21	1,0	0,2	1,0	[0;   12]	0,05	0,09	0,01
22	1,0	0,4	1,0	[0;   10]	0,05	0,09	0,01
23	0,5	0,0	50,0	[0;   12]	0,05	0,09	0,01
24	0,5	0,2	50,0	[0;   12]	0,05	0,09	0,01
25	0,5	0,4	50,0	[0;   10]	0,05	0,09	0,01
26	0,5	0,8	50,0	[0;     6]	0,05	0,09	0,01

2.2. Основные теоретические положения

          Из численных методов решения линейных, обыкновенных дифференциальных уравнений чаще всего на практике используют алгоритмы Рунге-Кутта и Адамса четвертого порядка точности с прогнозом