Исследование итерационных методов Ньютона и наискорейшего спуска решения нелинейной системы алгебраических уравнений

Лабораторная работа №5.

Решение систем нелинейных алгебраических уравнений

Цель работы

               Исследование итерационных методов Ньютона и наискорейшего спуска решения нелинейной системы алгебраических уравнений. Анализ влияния начальных условий и параметра останова на точность (количество итераций) определения корней, сравнение методов решения.

Постановка задачи

               Решить нелинейную алгебраическую систему уравнений:

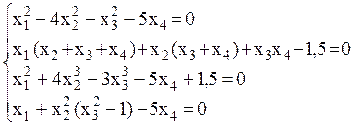
               Корни системы: =  2,0; = – 0,5; =  1,0; =  0,4.

Краткие теоретические сведения

Метод Ньютона. Если в некоторой области, содержащей решение
  системы

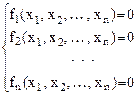
функции fi(x), i Î[1, n] непрерывны, имеют непрерывные частные производные и в точке x =  ( матрица

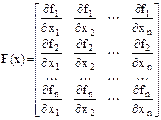
не вырождена, то решение может быть определено посредством итерационной

процедуры метода Ньютона

xk+1 = xk – F–1(xk)f(xk),   k = 0, 1, 2, ... ,

f(xk) = {f1(xk), f2(xk), ... , fn(xk)}.

               Условием сходимости метода Ньютона, помимо требований предъявляемых к функциям fi(x), iÎ [1, n] и матрице F(x), является соответствующий выбор начальных условий. Вектор x0 должен быть выбран достаточно близко к истинному решению x*.

               В лабораторной работе для решения нелинейной системы уравнений используется модификация приведенного метода Ньютона, в которой операция обращения матрицы заменяется процедурой решения системы n линейных алгебраических уравнений. Данный алгоритм реализуется в следующем виде

xk+1 = xk + Dxk,   k = 0, 1, 2, ... ,

а Dxk = xk+1 – xk представляет собой решение линейной системы

F(xk)Dxk = - f(xk),

полученной путем элементарных преобразований исходного алгоритма.

               Останов итерационной процедуры метода Ньютона можно осуществлять по соотношению

| | £ e,   k = 0, 1, 2, …,

где e > 0 – сколь угодно малое, наперед задаваемое число.

               Достоинством метода Ньютона является очень высокая скорость сходимости, а недостатком – большая чувствительность к начальным условиям, т.к. при их очень грубом задании алгоритм может разойтись или привести к другому решению.

               Метод наискорейшего спуска. Если функции fi(x), i Î[1, n], входящие в систему нелинейных уравнений являются непрерывными, вещественными функциями действительных переменных xi, i Î[1, n] и имеют непрерывные первые частные производные в области определения и только изолированные корни в этой области, то поиск решения такой системы можно свести к поиску минимума функционала

 ,

причем спуск из некоторой точки xk функционала Ф(x) в сторону его минимума может осуществляться в виде

xk+1 = xk + hkvk , k = 0, 1, 2, ...,

где vk – вектор, задающий направление движения, а hk – параметр, обеспечивающий уменьшение значения функционала Ф(x) на данной итерации по сравнению с предыдущей.

               В качестве вектора vk выбирается

- grad Ф(xk) = ,

т.к. именно в направлении этого вектора Ф(x) убывает с максимальной скоростью.

               Параметр hk, вообще говоря, необходимо определять из условия уменьшения максимальным образом значения функционала Ф(xk+1) на (k + 1)–й итерации по сравнению с Ф(xk) на k–той итерации, что требует достаточно существенных вычислительных затрат, поэтому в лабораторной работе производится лишь приближенный выбор параметра hk в виде

hk = .

Таким образом, градиентный метод наискорейшего спуска определяется соотношением

xk+1 = xk –{}grad Ф(xk),  k = 0, 1, 2, ... .

               Окончание итерационной процедуры производится по условию

½Ф(xk+1) – Ф(xk)½ £ e

или

½grad Ф(xk+1)½ £ e,

где e > 0 – сколь угодно малое, наперед задаваемое число.

               Метод наискорейшего спуска уступает методу Ньютона в скорости сходимости и простоте реализации (большое количество вычислительных операций, связанных с неоднократным определением частных производных при вычислении вектора градиента), однако в данном случае решение системы уравнений может быть найдено при более грубых начальных условиях.

Результаты работы

Таблица 1

Влияние нач. усл. (пар. DK)на точность и количество итераций метода Ньютона

 DK     EPS      lgEPS              Emo            lgEMO           Ec               lgEco        KM

 1.5  0.1D-02  -0.3D+01  0.2335D+01   0.368D+00  0.4041D+01   0.606D+00   13

 2.0  0.1D-02  -0.3D+01  0.2711D-06  -0.657D+01  0.2239D-06  -0.665D+01    9

 2.5  0.1D-02  -0.3D+01  0.1472D-05  -0.583D+01  0.1257D-05  -0.590D+01   21