1968 0.2000D+01 -0.5000D+00 0.1000D+01 0.4000D+00
1969 0.2000D+01 -0.5000D+00 0.1000D+01 0.4000D+00
1970 0.2000D+01 -0.5000D+00 0.1000D+01 0.4000D+00
Порядок системы N = 4
Система уравнений:
X1**2-4*X2**2-X3**2-5*X4=0
X1*X2+X1*X3+X1*X4+X2*X3+X2*X4+X3*X4-1.5 =0
X1**2+4*X2**3-3*X3**3-5*X4+1.5=0
X1+X2**2+X2**2*X3**2-5*X4-X2**2=0
Корни системы: 0.2000D+01 -0.5000D+00 0.1000D+01 0.4000D+00
Графики зависимостей
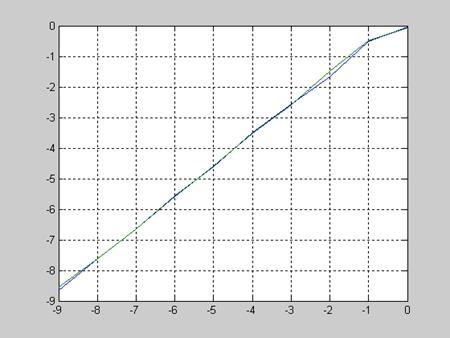
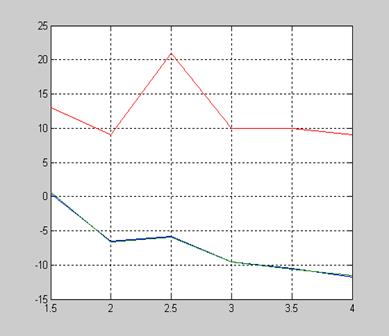
Рисунок 1 Рисунок 2
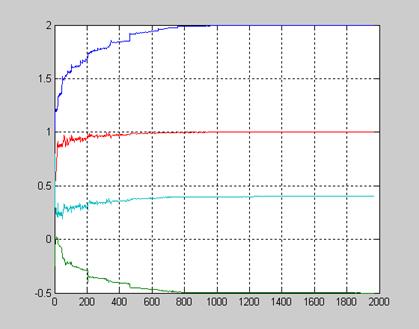
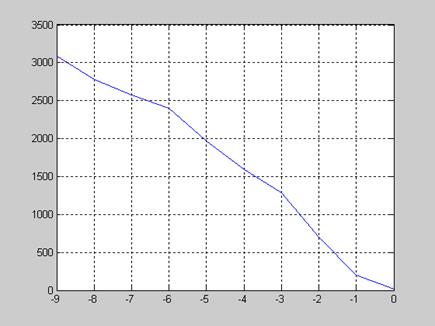
Рисунок 3 Рисунок 4
На рисунке 1 изображены графики lg
Eмо = f(DK) (lg Eсо = f(DK)), KM = f(DK), на рисунке 2 lg Eмо = f(lg e) (lg Eсо = f(lg EPS)), KM = f(lg EPS), а на
рисунке 3 ![]() = f(K), KÎ [0, KM], KM – количество итераций для
вычисления корней с заданными DK и EPS.
= f(K), KÎ [0, KM], KM – количество итераций для
вычисления корней с заданными DK и EPS.
Вывод
КМ у метода спуска гораздо больше чем у метода Ньютона, но зато точность примерно в два раза выше.
Проанализировали влияния начальных условий и параметра останова на точность (количество итераций) определения корней, сравнение методов решения.
Чем больше DK – коэффициент, задающий начальные значения оценок искомых корней системы, тем больше
· KM – количество итераций за которое определены оценки корней системы уравнений для заданного EPS
· EM – максимальная погрешность между истинными корнями системы и их оценками;
· EMO – максимальная относительная погрешность между истинными корнями системы и их оценками;
· ESO – среднеквадратичная относительная погрешность между истинными корнями системы и их оценками.
Чем меньше параметр EPS тем больше количество итераций, притом для метода Спуска их на порядок больше, чем для метода Ньютона
Пиложение
Листинг программы
character*64 name
integer nv,n,nn,km
real*8 xi(9),x(9),df(99),f(99),dx(9)
real*8 dk,eps,em,emo,eso
eps=0.001
nv=6
name='sx.dat'
open(13,FILE='1n.txt')
write(13,*) 'DK EPS lgEPS Emo lgEMO Eco lgECO
* lgEco KM'
dk=1.5
1 call n1yiru(nv,n,xi)
call n1ynu(n,xi,dk,x)
call n1yntm(nv,n,x,eps,nn,df,f,dx,km,name)
call n1ypgr(n,xi,x,em,emo,eso)
write(13,10) dk,eps,log10(eps),emo,log10(emo),eso,log10(eso),km
dk=dk+0.5
if(dk.LE.4) GOTO 1
close(13)
dk=2
eps=1D-9
open(13,FILE='2n.txt')
write(13,*) 'DK EPS lgEPS Emo lgEMO Eco lgECO
* lgEco KM'
do 2 i=1,10
call n1yiru(nv,n,xi)
call n1ynu(n,xi,dk,x)
call n1yntm(nv,n,x,eps,nn,df,f,dx,km,name)
call n1ypgr(n,xi,x,em,emo,eso)
write(13,10) dk,eps,log10(eps),emo,log10(emo),eso,log10(eso),km
eps=eps*10
2 continue
close(13)
dk=2
eps=1D-5
name='1n.dat'
call n1yiru(nv,n,xi)
call n1ynu(n,xi,dk,x)
call n1yntm(nv,n,x,eps,nn,df,f,dx,km,name)
call n1ypgr(n,xi,x,em,emo,eso)
name='sx.dat'
eps=0.001
nv=6
name='sx.dat'
open(13,FILE='1s.txt')
write(13,*) 'DK EPS lgEPS Emo lgEMO Eco lgECO
* lgEco KM'
dk=1.5
5 call n1yiru(nv,n,xi)
call n1ynu(n,xi,dk,x)
call n1ynsm(nv,n,x,eps,df,km,name)
call n1ypgr(n,xi,x,em,emo,eso)
write(13,10) dk,eps,log10(eps),emo,log10(emo),eso,log10(eso),km
dk=dk+0.5
if(dk.LE.4) GOTO 5
close(13)
dk=2
eps=1D-9
open(13,FILE='2s.txt')
write(13,*) 'DK EPS lgEPS Emo lgEMO Eco lgECO
* lgEco KM'
do 6 i=1,10
call n1yiru(nv,n,xi)
call n1ynu(n,xi,dk,x)
call n1ynsm(nv,n,x,eps,df,km,name)
call n1ypgr(n,xi,x,em,emo,eso)
write(13,10) dk,eps,log10(eps),emo,log10(emo),eso,log10(eso),km
eps=eps*10
6 continue
close(13)
dk=2
eps=1D-5
name='1s.dat'
call n1yiru(nv,n,xi)
call n1ynu(n,xi,dk,x)
call n1ynsm(nv,n,x,eps,df,km,name)
call n1ypgr(n,xi,x,em,emo,eso)
name='sx.dat'
10 format(F4.1,D9.1,D10.1,D12.4,D12.3,D12.4,D12.3,I5)
end
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.