Исследование итерационного метода "золотого сечения" решения задачи одномерной оптимизации. Анализ влияния начальной длины интервала неопределенности и параметра останова итерационной процедуры на точность (количество итераций) определения оптимального значения проектного параметра.
Найти оптимальное значение x* проектного параметра x, при котором целевая функция u(x), x Î[a, b] имеет минимальное значение.
Вид целевой функции:
5) u(x) = x4 – 43x3 + 625x2 – 3350x + 20000,
x*1 = 4,41940, x*2 = 15,94756;
Метод золотого сечения
Метод золотого сечения является одним из самых эффективных методов одномерной оптимизации, используемых при решении практических задач. Последовательное уменьшение интервала неопределенности осуществляется за счет вычисления целевой функции на каждом шаге (кроме первого) лишь в одной, выбираемой специальным образом, точке, которая называется золотым сечением. Геометрически это иллюстрирует рисунке 1, где ищется минимум целевой функции. Пусть на нулевом шаге длина интервала неопределенности [a,b] задана в виде d = b – a = x20 – x 10 . Внутри [a,b] выбираются две точки x1 и x2 и вычисляются u(x1) и u(x2). Оказывается, что u(x1) < u(x2), следовательно, искомый минимум располагается между x11 = x10 и x21 = x2 . В полученном новом интервале неопределенности [x11,x21] длиной d1 = x21 – x11 необходимо опять выбрать две точки, но одна из них x1 уже есть, поэтому выбирается точка x3 и вычисляется u(x3) < u(x1). Границы нового интервала неопределенности x12 = x1, x22 = x21, а d2 = x22 –x12 .
|
Рисунок 1 |
Описанная процедура продолжается до тех пор пока не будет выполнено соотношение
dk = x2k – x1k £ e×d0, k = 0, 1, 2, ....
Точка золотого сечения выбирается из условия
l2/ l = l1/ l2 ,
где l = l1 + l2 представляет собой длину интервала неопределенности. Проделав элементарные преобразования с приведенным выше соотношением
![]()
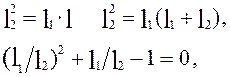
получим
l1 = r1×l, r1 = (3 – ![]() )/2 » 0,381966,
)/2 » 0,381966,
l2 = r2×l, r2 = (![]() – 1)/2 » 0,618034.
– 1)/2 » 0,618034.
Таким образом, метод золотого сечения можно представить в виде итерационного процесса, на каждом k–ом (k = 1, 2, ...) шаге которого выполняются следующие операции:
1) определяется k–е значение x1k в виде
x1k = x1(k–1) + r1×d(k–1)
и вычисляется u1k = u(x1k);
2) определяется k–е значение x2k в виде
x2k = x2(k–1) + r2×d(k–1)
и вычисляется u2k = u(x2k);
3) определяется k–й интервал неопределенности [x1k, x2k] согласно следующим соображениям
– если u1k £ u2k, то принимается x1k = x1(k–1), а x2k вычислено в операции 2),
– если u1k > u2k, то принимается x2k = x2(k–1), а x1k вычислено в операции 1);
4) находится длительность k–го интервала неопределенности
dk = x2k
– x1k = ![]() ×d0
×d0
и производится сравнение
– если dk > e×d0, то осуществляется переход на (k + 1)–й шаг,
– если dk £ e×d0, то итерационный процесс заканчивается, полагается
dl = x2k
– x1k и оптимальное значение проектного параметра определяется в
виде
x* = dl / 2. ![]()
![]()
Результаты вычислений
u(x)=x**4-43x**3+625x**2-3350x+20000, xi=4,4194
Таблица 1
Вид целевой функции:
N x u(x)
1 2.2097 0.1521D+05
2 2.2747 0.1513D+05
3 2.3397 0.1506D+05
4 2.4047 0.1499D+05
5 2.4697 0.1493D+05
6 2.5347 0.1487D+05
7 2.5996 0.1481D+05
8 2.6646 0.1475D+05
9 2.7296 0.1469D+05
10 2.7946 0.1464D+05
11 2.8596 0.1459D+05
12 2.9246 0.1455D+05
13 2.9896 0.1450D+05
14 3.0546 0.1446D+05
15 3.1196 0.1442D+05
16 3.1846 0.1438D+05
17 3.2496 0.1435D+05
18 3.3145 0.1432D+05
19 3.3795 0.1429D+05
20 3.4445 0.1426D+05
21 3.5095 0.1423D+05
22 3.5745 0.1421D+05
23 3.6395 0.1419D+05
24 3.7045 0.1417D+05
25 3.7695 0.1415D+05
26 3.8345 0.1414D+05
27 3.8995 0.1412D+05
28 3.9645 0.1411D+05
29 4.0294 0.1410D+05
30 4.0944 0.1409D+05
31 4.1594 0.1408D+05
32 4.2244 0.1408D+05
33 4.2894 0.1407D+05
34 4.3544 0.1407D+05
35 4.4194 0.1407D+05
36 4.4844 0.1407D+05
37 4.5494 0.1407D+05
38 4.6144 0.1408D+05
39 4.6794 0.1408D+05
40 4.7444 0.1409D+05
41 4.8093 0.1410D+05
42 4.8743 0.1411D+05
43 4.9393 0.1411D+05
44 5.0043 0.1413D+05
45 5.0693 0.1414D+05
46 5.1343 0.1415D+05
47 5.1993 0.1416D+05
48 5.2643 0.1418D+05
49 5.3293 0.1420D+05
50 5.3943 0.1421D+05
51 5.4593 0.1423D+05
52 5.5242 0.1425D+05
53 5.5892 0.1427D+05
54 5.6542 0.1429D+05
55 5.7192 0.1431D+05
56 5.7842 0.1433D+05
57 5.8492 0.1435D+05
58 5.9142 0.1438D+05
59 5.9792 0.1440D+05
60 6.0442 0.1442D+05
61 6.1092 0.1445D+05
62 6.1742 0.1447D+05
63 6.2391 0.1450D+05
64 6.3041 0.1453D+05
65 6.3691 0.1455D+05
66 6.4341 0.1458D+05
67 6.4991 0.1461D+05
68 6.5641 0.1463D+05
69 6.6291 0.1466D+05
70 6.6941 0.1469D+05
71 6.7591 0.1472D+05
72 6.8241 0.1475D+05
73 6.8891 0.1478D+05
74 6.9540 0.1481D+05
75 7.0190 0.1484D+05
76 7.0840 0.1487D+05
77 7.1490 0.1489D+05
78 7.2140 0.1492D+05
79 7.2790 0.1495D+05
80 7.3440 0.1498D+05
81 7.4090 0.1501D+05
82 7.4740 0.1504D+05
83 7.5390 0.1507D+05
84 7.6040 0.1510D+05
85 7.6690 0.1513D+05
86 7.7339 0.1516D+05
87 7.7989 0.1519D+05
88 7.8639 0.1522D+05
89 7.9289 0.1525D+05
90 7.9939 0.1528D+05
91 8.0589 0.1531D+05
92 8.1239 0.1533D+05
93 8.1889 0.1536D+05
94 8.2539 0.1539D+05
95 8.3189 0.1542D+05
96 8.3839 0.1545D+05
97 8.4488 0.1547D+05
98 8.5138 0.1550D+05
99 8.5788 0.1553D+05
100 8.6438 0.1555D+05
101 8.7088 0.1558D+05
Таблица 2
Сходимость алгоритма GLS
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.