Задача 6
Пусть задана платежная матрица затрат при 5 стратегиях поведения и 6 альтернативах (табл. 7). Требуется выбрать наилучшее решение по критерию затрат.
Таблица 7. Исходные данные задачи
|
Варианты ( альтернативы), i |
|||||||
|
Стратегии, j |
№1 |
№2 |
№3 |
№4 |
№5 |
№6 |
|
|
S1 |
12 |
20 |
40 |
35 |
25 |
35 |
|
|
S2 |
20 |
35 |
49 |
30 |
18 |
12 |
|
|
S3 |
60 |
30 |
35 |
40 |
12 |
50 |
|
|
S4 |
30 |
18 |
20 |
30 |
35 |
45 |
|
|
S5 |
45 |
25 |
18 |
50 |
50 |
15 |
|
Решение. Для выбора наиболее эффективного решения в условиях неопределенности рекомендуется применять следующие критерии выбора:
ü Критерий Байеса- Лапласа: из множества допустимых решений выбирают наиболее оптимальное согласно следующему выражению:
![]() W opt=
W opt= 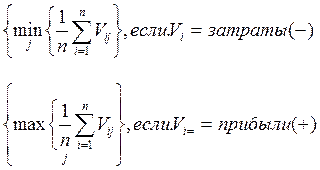 .
.
1. В соответствии с приведенным выражением проведем рассчет:
P= 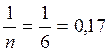 ;
;
W1 = 0,17 (12+20+40+35+25+35) = 28,4;
W2 = 0,17 (20+35+49+30+18+12) = 27,9; где красный –по прибыли
W3 = 0,17 (60+30+35+40+12+50)=38,6; зеленый- по затратам
W4 = 0,17 (30+18+20+30+35+45)=30,3;
W5 = 0,17 (45+25+18+50+50+15)=34,5.
ü Критерий Вальда: из множества наихудших стратегий (ситуации) следует выбирать наилучшую.
![]()
Wopt= 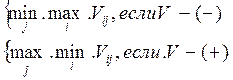
2. Проведенные расчеты сведены в табл.8.
Таблица 8. Расчеты по критерию Вальда
|
Варианты ( альтернативы), i |
|||||||||
|
Стратегии, j |
№1 |
№2 |
№3 |
№4 |
№5 |
№6 |
min |
Max |
|
|
S1 |
12 |
20 |
40 |
35 |
25 |
35 |
12 |
40 |
|
|
S2 |
20 |
35 |
49 |
30 |
18 |
12 |
12 |
49 |
|
|
S3 |
60 |
30 |
35 |
40 |
12 |
50 |
12 |
60 |
|
|
S4 |
30 |
18 |
20 |
30 |
35 |
45 |
18 |
45 |
|
|
S5 |
45 |
25 |
18 |
50 |
50 |
15 |
15 |
50 |
|
ü Критерий Гурвица
учитывает склонность человека к риску путем введения
коэффициента доверия ![]() :
: ![]() Î
Î ![]() ;
; ![]() = 0¸0,5 – пессимист;
= 0¸0,5 – пессимист; ![]() 0=
0,51¸1,0 0 - оптимист.
0=
0,51¸1,0 0 - оптимист.
![]() W opt =
W opt = 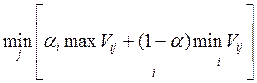 min Vij, если V-затраты
min Vij, если V-затраты
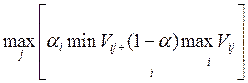 , если V-(+)
, если V-(+)
В крайнем случае критерий Гурвица превращается в критерий Вальда.
3.Пусть ![]() = 0,3, тогда рассчитаем:
= 0,3, тогда рассчитаем:
|
По затратам: |
По прибыли: |
|
W1= 0,3 |
W1= 0,3 |
|
W2=0,3 |
W2= 0,3 |
|
W3=0,3 |
W3= 0,3 |
|
W4=0,3 |
W4=0,3 |
|
W5=0,3 |
W4=0,3 |
ü Критерий Сэвиджа
рекомендует матрицы затрат (прибыли) преобразовать в матрицы риска по следующему правилу:
Vij - 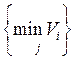 , если +(-)
, если +(-)
|
По затратам |
По прибыли |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]() если
(+). Таблица 9
если
(+). Таблица 9
Вывод : Наилучшее решение – стратегия S2, обеспечивающая получение максимальной прибыли и минимальных затрат.
Список литературы:
1. Арсеньев Ю.Н., Шелобаев С.И. Оптимизация банковских процессов и принятия решений. – М.: Высшая школа, 1999. – 604 с.
2. Арсеньев Ю.Н., Шелобаев С.И. Методы и модели оптимизации ресурсов субъекта рынка. – М.: Высшая школа, 1999. – 604 с.
3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.