Определение коэффициента конкордации

Задача №2

Пусть число экспертов равно 8. Число оцениваемых ими товаров равно 10. Определить коэффициент конкордации.

Решение. Выполненные экспертами оценки представим в табл. 4.

Таблица 4. Оценки товаров, выполненные экспертами

1.  По данным табл. 4 определим ранг (сумму мест товара):r_i = , j= .

2.  Определим среднее число а: ,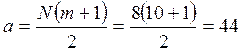

3.  Определим расстояние  d_i = .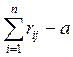

3. Вычислим расстояние R(d)² = .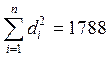

4. Степень согласия экспертов равен:

R_mах(d²) = N (m³-m) = .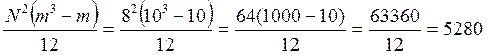

5.Найдем коэффициент конкордации, как показатель степени согласованности мнений экспертов относительно важности заданных товаров:

W = 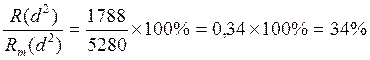, т.е. риск довольно высок.

6. Находим согласованность экспертов по критерию  по формуле:

           ,  .

По справочной таблице ищем табличное значение _табл при 9 степенях свободы (n = m – 1 = 9) равно _{табл =}  10,7.

Вывод: Если полученное расчетное значение > , то коэффициент конкордации W, или степень согласованности экспертов, значимы.