Пусть даны 10 товаров, для оценки качества которых приглашены два эксперта. Определить степень согласия экспертов по коэффициенту парной ранговой корреляции.
Решение. Пусть эксперты определяют качество товара согласно табл. 5. Сведем промежуточные расчеты также в эту таблицу.
|
Эксперт,N |
Товары, m |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1 |
5 |
3 |
6 |
1 |
4 |
2 |
4 |
2 |
6 |
1 |
|
2 |
3 |
7 |
7 |
5 |
1 |
3 |
7 |
6 |
1 |
2 |
|
di |
2 |
-4 |
-1 |
-4 |
3 |
-1 |
-3 |
-4 |
5 |
-1 |
|
di2 |
4 |
16 |
1 |
16 |
9 |
1 |
9 |
16 |
25 |
1 |
|
R(d)2 |
98 |
|||||||||
1. Определим расстояние между рангами (местами) расположения товаров со стороны экспертов по следующей формуле:
di= r1i - r2i.
2. Определим R(d)2 = = 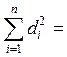 98.
98.
1. Находим коэффициенты парной ранговой корреляции по формуле:
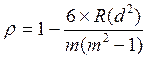 ,
,
где m- число товаров.
![]() 1 -
1 - 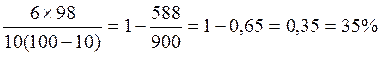
![]()
Вывод: Так как мера близости ранжировок
низка, то эксперты существенно расходятся в мнениях, и риск ситуации достаточно
высок, .![]() Î
Î ![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.