Коэффициент корреляции Спирмена. Понятие ложной корреляции для закрытых числовых систем. Геометризация пластовых залежей. Вероятностные системы и их элементы. Вероятностные структуры и их свойства.

1. Коэффициент корреляции Спирмена. Понятие ложной корреляции для закрытых числовых систем. Понятие множественной корреляции.

Зависимость при которой изменение одной из случайных величин вызывает изменение другой, называется статической (стохастической).  При стохастической зависимости различают корреляцию, когда устанавливают существование взаимосвязи между двумя или более случайными величинами и оценивают силу (тесноту) этой связи, и регрессию, когда выясняют характер (форму)  зависимости между величинами Х и У, и возможность оценки У по Х ( или Х по У), причем  либо Х или У, либо Х и У являются случайными величинами. Оценка тесноты связей производится путем расчета коэффициента корреляции, определяющего и степень взаимосвязи между случайными величинами.

В тех случаях, когда определяется взаимосвязь между случайными величинами Х и У, распределенному не по нормальному закону, а произвольно, зависимость между Х и У оценивается с помощью коэффициентов корреляции Спирмена и Кендалла. Для первого из них величина

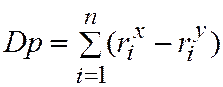
где r_i^х и r_i^у – ранги соответствующих значений Х и У, используемые тогда, когда совпадающие значения Х и У отсутствуют в противном  случае применяют формулу

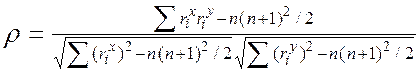
Коэффициенты равной корреляции Спирмена и Кендалла также используются при построении эффективных алгоритмов обнаружения слабых сигналов.

Если многомерная случайная величина включает не две, а большее число компонент, т.е. если изучаются связи между несколькими признаками, число которых выше двух то такая корреляция называется множественной.

Рассмотрим случай, когда число компонент многомерной величины равно трем и связь между ними линейная: z_xy=ax+by+c. В этом случае возникают следующие задачи:

1) по данным выборки найти коэффициенты регрессии а, b и параметр с;

2) оценить тесноту связи между  z  и обеими другими компонентами x и y;

3) оценить тесноту связи между z и х (при постоянном у) и между z и у (при постоянном х).

Для решения первой задачи уравнение регрессии z на х и у ищется аналогично:

z`<sub>xy</sub>-z`= a(x-x`)+b(y-y`),

,

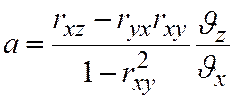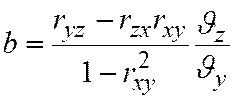
Здесь r_xz, r_yz, r_xy -  коэффициенты корреляции между х и z, у и z, х и у. Они вычисляются как обычные коэффициенты для двумерной случайной величины и называются парными коэффициентами корреляции. Величины θх, θу, θz есть не что иное, как средние квадратические отклонения величин х, у, z.

Теснота зависимости z от х и у одновременно оценивается совокупным или множественным коэффициентом корреляции R, который определяется также через парные коэффициенты корреляции:

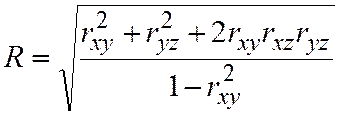
Характер и содержание связей между несколькими переменными значительно сложнее, чем в случае только двух переменных.

2.Геометризация пластовых залежей.

Геометрия, как и вообще математика, изучает пространственные отношения и формы тел, не касаясь всех прочих свойств реальных объектов. В та­ком понимании геометрия изучает фигуры тел, их взаимное рас­положение и размеры их частей, а также преобразования фигур, т. е. некоторые отношения между двумя фигурами—данной и той, в которую она преобразуется. В последующем развитии гео­метрии ее предметом стали не только пространственные, но и вообще любые отношения и формы, которые возникают при рас­смотрении однородных объектов, явлений, событий вне их конкрет­ного содержания и которые оказываются сходными с обычными пространственными отношениями и формами.

Обычное реальное пространство понимают в геометрии как не­прерывную совокупность точек, т. е. всех возможных предельно точно определенных местоположений предельно малого тела.

Аналогично непрерывную совокупность возможных состояний какой-либо материальной системы, непрерывную совокупность каких-либо однородных явлений можно также трактовать как сво­его рода пространство. Если состояние какой-либо системы определяется n величинами, то говорят что о n-мерном пространстве. Если число величин, характеризующих состояние системы, не превышает трех (n<=З), то возможно графическое изображение процессов и закономерностей. При n>3 наглядное графическое представление уже невозможно.

В нефтегазовой геологии все построения проводятся в евклидо­вом, т. е. трехмерном, пространстве, представляющем собой част­ный случай метрического пространства. Геологические тела и их границы изображаются при этом в декартовой (прямоугольной, ортогональной) системе координат.

Геометрические свойства геологических тел используются глав­ным образом для построения полноопределенного пространства. Решение этой задачи начинается с корреляции разрезов скважин. При проведении границ используется операция интерполяции в евкли­довом пространстве, когда по декартовым координатам границы в двух фиксированных точках формального пространства предска­зывается ее положение в любой промежуточной точке.