





Тема 5: Корреляционно-регрессионный анализ
Существует ряд задач, в которых важно установить как зависит изучаемая случайная величина Y от одного или нескольких изменяемых параметров (x1, x2, …, xn). Значение таких зависимостей необходимо как для предсказания результатов при изменении условий протекания процесса, так и для оптимизации какого-либо процесса или материала.
Корреляционными зависимостями пользовались всегда: все народные приметы построены на корреляциях, не говоря уже о современной науке. Вы выходите из дома и, чтобы узнать будет ли дождь – вы смотрите на барометр. Если давление падает ниже чем 700 мм. рт. ст., то существует большая вероятность дождя, потому что существует корреляция давление – осадки. Как можно определить есть ли нефть или газ на глубине без дорогостоящих буровых скважин или как можно заранее предсказать землетрясение? По коррелируемым с этим явлением факторам. Задачи определения состава, рецептуры, технологии решаются через построение корреляций; причем независимо, нужна вам рецептура для торта или рецепт небьющегося стекла.
Определения:
Случайные величины могут быть (1) независимыми, либо (2) связанными статистической зависимостью.
О статистической зависимости говорят тогда, когда изменение одной из величин приводит к изменению распределения другой. Статистическую зависимость называют корреляционной, если при изменении одной из величин изменяется среднее значение другой (при этом каждому значению независимой переменной x соответствует неопределённое количество значений отклика Y, или наоборот). Частный случай корреляционной зависимости, когда каждому значению x соответствует только одно значение Y и наоборот, называют функциональной зависимостью.
Корреляционный анализ изучает закон поведения случайной величины (Y) в зависимости от других величин (x1, x2, …, xn), а также меру зависимости (тесноту связи) между рассматриваемыми величинами, другими словами, степень приближения корреляционной зависимости к функциональной.
Классификация.
Корреляция может быть:
(1) парной: случай, когда изучается зависимость между двумя переменными x и y;
(2) множественной: когда рассматривается зависимость между зависимой переменной y и группой независимых переменных x1, x2, …, xn.
Формы представления корреляционной зависимости.
Корреляционная зависимость может быть представлена в виде (1) корреляционной таблицы, (2) поля корреляции, (3) аналитически (в виде математической формулы).
1. Корреляционная таблица – таблица, в строке которой указывают значения x, в столбце – значение y, а на пересечении строк и столбцов – частоты nxy наблюдаемых пар (xi, yi).
|
x y |
x1 |
x2 |
… |
xn |
|
y1 |
nxy |
|||
|
y2 |
||||
|
… |
||||
|
ym |
||||
2. Поле корреляции – это совокупность точек в прямоугольной системе координат, каждая из которых графически изображает отдельную пару значений (x, y). Структкра поля корреляции свидетельствует о степени корреляционной зависимости
![]()
![]()
 .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 Пр(1). Если
точки y
y y
Пр(1). Если
точки y
y y
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() рассеяны равномерно,
рассеяны равномерно,
![]()
![]()
![]()
![]() то это
означает, что
то это
означает, что
![]()
![]()
![]() переменные
являются
переменные
являются
независимыми (рис.
а). ![]() x
x ![]() x
x ![]() x
x
Пр(2). Если точки (a) (б) (в)
группируются вдоль некоторых линий, то это указывает на существование зависимости между этими двумя переменными (рис. б и в). В случае, когда такой линией будет прямая, можно говорить о наличии линейной зависимости (рис. б).
После представления понятия «поле корреляции», легко себе представить, что же означает коэффициент корреляции. Проследим такую процедуру:
Если
(1) поле корреляции разделить на четыре квадранта при помощи
среднеквадратических ![]() и
и ![]() ; (2) для каждой точки (xi, yi) найти произведение отклонений xi и yi от их средних, т.е.
; (2) для каждой точки (xi, yi) найти произведение отклонений xi и yi от их средних, т.е. ![]() ;
(3) просуммировать произведения отклонений для всех точек xi и yi.
;
(3) просуммировать произведения отклонений для всех точек xi и yi.
В
итоге эта сумма 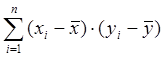 будет тем больше, чем теснее
связь между переменными; и она будет близкой к нулю, когда отсутствует
зависимость между x и y. (Пр.1 – т.к. величины
отрицательных и положительных отклонений компенсируют друг друга). Т.о. эта
сумма может являться характеристикой тесноты связи между x и y.
Если разделить эту сумму на количество наблюдений n и
среднеквадратичные отклонения sх и sу, то получим коэффициент корреляции ryx.
будет тем больше, чем теснее
связь между переменными; и она будет близкой к нулю, когда отсутствует
зависимость между x и y. (Пр.1 – т.к. величины
отрицательных и положительных отклонений компенсируют друг друга). Т.о. эта
сумма может являться характеристикой тесноты связи между x и y.
Если разделить эту сумму на количество наблюдений n и
среднеквадратичные отклонения sх и sу, то получим коэффициент корреляции ryx.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.