Методы поисковой оптимизации. Метод Гаусса-Зайделя. Метод крутого восхождения Бокса-Уилсона

Тема         7:             Методы поисковой оптимизации

Главной целью большинства исследований является достижение наилучших показателей (при разработке рецептуры материала, технологии процесса и т. д.).

Оптимизацией называется процесс нахождения наилучших значений целевой функции y (критерия оптимизации).

Если критерий оптимизации у есть функция входных управляемых параметров x₁, x₂,...,x_n :

у=f(x₁, x₂,...,x_n)

где n- число факторов, то задача оптимизации сводится к отысканию таких значений факторов

,

при которых целевая функция у достигает экстремума (минимума или максимума).

Решение, т.е. отыскание вектора  может быть аналитическим (1) и экспериментальным (2).

(1). В случае, когда целевая функция у задана используют известное свойство функций, имеющих экстремум, а именно, в точке экстремума первая производная этой функции обращается в ноль. Таким образом, для n-факторного пространства, чтобы найти вектор , находят n частных производных по каждому из n-факторов и решают систему уравнений:

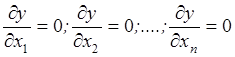
(2). В случае, когда целевая функция у неизвестна  используют экспериментальные методы поисковой оптимизации, основными из которых являются:

а) метод Гаусса-Зайделя;

б) метод градиента;

в) метод крутого восхождения Бокса-Уилсона;

г) симплексный метод.

Каждый из методов включает в себя 2 процедуры:

(а) определение направления движения к экстремуму с помощью пробных опытов;

(б) «рабочее» движение в сторону экстремума.

1.  Метод Гаусса-Зайделя.

Метод Гаусса-Зайделя предусматривает поочерёдное нахождение частных экстремумов целевой функции по каждому фактору x_i ( i=1,2,…,n ). При этом на каждом i-м этапе стабилизируют n-1 факторов и варьируют только один i-й фактор.

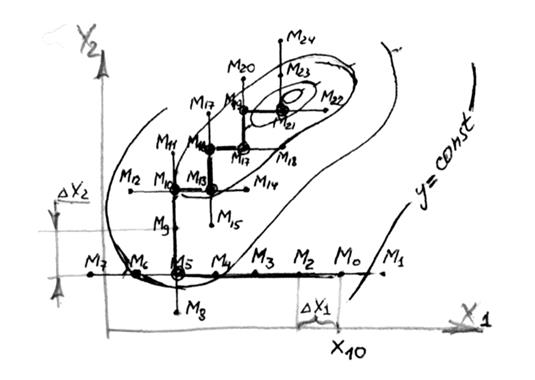
Рис. Метод Гаусса-Зайделя

Графическая интерпретация метода дана на рисунке на примере двух факторов x₁ и x₂ . Функция отклика у изображена топографическим способом с помощью замкнутых линий постоянного уровня у (у=const).

До начала исследований форма функции отклика, естественно, неизвестна, т. е. исследователь на момент планирования не видит этих линий. (Они видны на рисунке, чтобы понять как работает метод). Путь движения обозначен точками М. Задачу поиска максимума решают в несколько этапов:

Этап I: Поиск частного экстремума при движении по х₁ со стабилизацией всех остальных факторов.

1.1  Выбор начальной точки М₀ ( х₁₀; х₂₀;…; х_n0 )

      (чаще в центре области исследования)

1.2  Выбор интервала варьирования х₁ по фактору х₁. Размер х₁ определяет скорость движения к экстремуму.

1.3  Определение координаты пробных точек М₁ (х₁₀+х₁; х₂₀;…; х_n0) и М₂(х₁₀-х₁; х₂₀;…;х_n0).

1.4  Определение у(М₁) и у(М₂) в результате проведения пробных опытов.

1.5  Определение направления движения в сторону большего у(М_i): например, если у(М₂)> у(М₁), то рабочее движение совершают на один шаг по направлению вектора  в точку М₃.

1.6  Продолжение движения аналогичным образом продолжается до реализации условия у(М_к)< у(М_к-1), которое указывает на достижение частного экстремума в точке М_к-1. На рисунке это М₅.

Этап II: Поиск частного экстремума при движении по х₂ со стабилизацией всех остальных факторов.

Порядок проведения поиска тот же, что и для этапа I. За новую базовую точку принимают М_к-1(х₁₀±х_1*(к-2); х₂₀;…; х_n0), а х₂ варьируют на х₂. После достижения частного экстремума по фактору х₂ , точку нового экстремума принимают за новую базовую точку. На рисунке это М₁₀.

Первый цикл продвижения к экстремуму заканчивается n-м этапом, на котором стабилизируют все факторы, кроме х_n. Если экстремум не достигнут, то выполняют следующий цикл поиска по аналогичной схеме.

Экстремум считается достигнутым, если при движении в любую сторону по всем  n-факторным осям значения отклика y оказываются меньшими.

Достоинства метода Гаусса-Зайделя: простота и наглядность.

Недостатки: (1) слишком долгий путь к главному экстремуму, особенно при большом числе факторов n; (2) метод не даёт информации о взаимодействиях факторов.

2. Метод градиента

Сущность метода заключается в том, что направление движения к экстремуму задаёт направление градиента. Вектор-градиент в n–факторном пространстве определяется соотношением

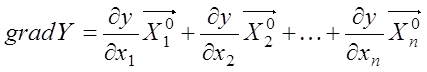
где  - частная производная целевой функции y по i – му фактору;

- единичные направляющие векторы, расположенные вдоль факторных осей.

x1

x10

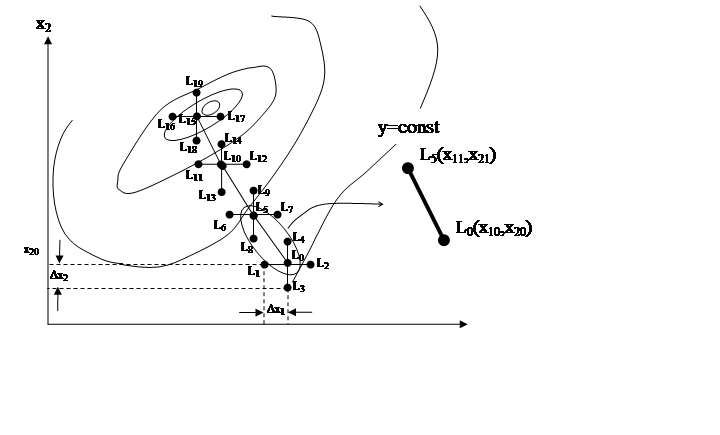
Рис. Метод градиента

Последовательность метода

1.1       Выбор начальной точки L₀(X₁₀,X₂₀,..,X_n0)

(Методика выбора одинакова для всех методов).

1.2       Выбор интервала варьирования  ΔX_i по каждому фактору

(Методика выбора одинакова для всех методов).

1.3    Определение координат пробных точек. Пробные точки выбираются вдоль направлений всех факторных осей. В случае двух-факторного пространства это четыре точки:

L₁(X₁₀- ΔX₁; X₂₀);                 L₂(X₁₀+ΔX₁; X₂₀);

L₃(X₁₀; X₂₀- ΔX₂);                 L₄(X₁₀; X₂₀+ ΔX₂);

1.4 Определение целевой функции y в пробных точках, в результате проведения опытов.

1.5 Определение координат рабочей точки L(X₁₁,X₂₁,..,X_n1) на направлении градиента. Для рассматриваемого примера координаты  L₅(x₁₁,x₂₁) рассчитываются по формуле:

                                                           X_i1 = X_i0 + r_грa_i0,

где Х_i0- координата базовой точки L₀ по i-му фактору;

ρ_гр- параметр рабочего шага; назначается исследователем;

а_i0- оценка вектор-градиента в точке L₀ для каждого i-го фактора:

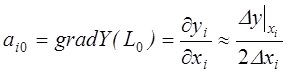
В частности для факторов х₁ и х₂ вычисление а₁₀ и а₂₀ производится по формулам:

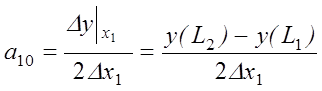
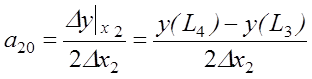
1.6. Повторение цикла, состоящего из пп. 1.3 - 1.5 (проведение новых пробных опытов /оценивание нового направления градиента / рабочий шаг в точку с координатами X_{i, k+1} = X_ik + r_грa_ik).

1.7 Рабочее движение производят до тех пор пока составляющие градиента не станут пренебрежимо малыми, т. е. все а_i,к+10. В рассматриваемом примере за экстремум принимают точку L₁₅ (рис.)

Достоинства метода градиента : (1) простота; (2) повышенная по сравнению с методом Гаусса-Зайделя скорость движения к экстремуму (эффективность).