Недостатки : (1) в случае сложной формы поверхности отклика этот метод может не привести к истинному экстремуму; (2) метод не даёт информации о взаимодействии факторов (взаимодействия характеризуют степень кривизны поверхности отклика).
3. Метод крутого восхождения Бокса- Уилсона
Метод крутого восхождения предложен Боксом и Уилсоном как синтез лучших черт метода градиента и метода Гаусса - Зайделя, причем пробные опыты выполняют с помощью ПФП или ДФП.
От метода градиента взято выполнение рабочего движения вдоль вектор - градиента.
От метода Гаусса - Зайделя взят принцип продвижения не на один рабочий шаг (как в методе градиента), а до достижения частного экстремума функции отклика на направлении градиента.
Использование ПФП (ДФП) позволяет: 1) более точно оценивать направление градиента; 2) получить информацию о взаимодействии факторов.
 |
 |
|||||||||
 |
|||||||||
 |
|||||||||
 |
|||||||||
 |
|||||||||
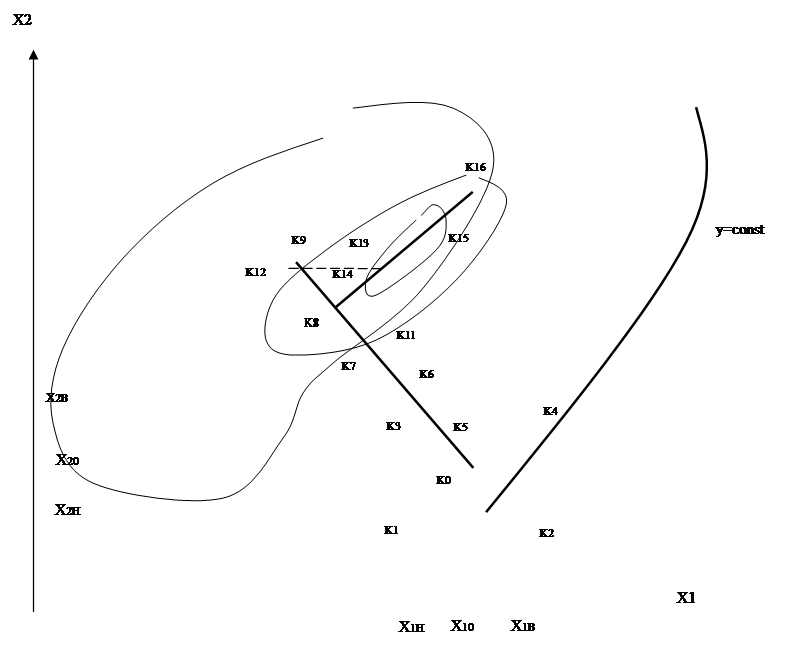
Рис. Метод крутого восхождения Бокса- Уилсона
Последовательность метода
1.1. Выбор начальной точки К0 (Х10,Х20,…,Хn0) (методика выбора одинакова для всех методов).
1.2.
Выбор интервала варьирования 
по
каждому фактору (методика выбора одинакова для всех факторов).
1.3.
Определение координат пробных точек. Количество пробных опытов 
(в случае ПФП) и 
(в случае ДФП). Координаты верхнего и
нижнего уровней находят из соотношений:
XiB =Xi0+
Xi; XiH =Xi0-Xi;
Для примера
рассмотренного на рисунке, количество факторов равно двум, количество пробных
опытов
(точки К1 –
К4).
1.4. Определение целевой функции y в пробных точках в результате проведения опытов.
1.5. Определение координат k-х рабочих точек (к=1,2,…) на направлении градиента осуществляется по формуле:
где Xio – координаты базовой точки K0 по i-му фактору
K - количество рабочих точек на направлении градиента до достижения частного экстремума. Для рассматриваемого примера это точки K5 - K9 (рисунок).
aio – оценка вектор- градиента в точке Lo для каждого i-го фактора расчитывается аналогично, как в методе градиента:
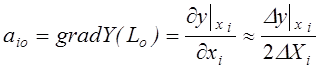
- параметр рабочего шага.
1.6. Признаком достижения частного экстремума является уменьшение отклика в последующих опытах.
Точку
частного экстремума (на рисунке точка К8) принимаем за новую базовую точку и
организуют следующий цикл крутого восхождения (пп 1.3.-1.5.). Последующие циклы
отличаются от предыдущих размером интервала варьирования xi и рабочих шагов, которые выбирают меньшими по мере приближения к
экстремуму и с увеличением кривизны поверхности отклика.
1.7. Поисковое рабочее движение прекращают при достижении области экстремума. Признаком достижения области экстремума является статистическая незначимость оценок аi .
Достоинства метода кругового восхождения:
1) высокая помехоустойчивость, связанная с высокой точностью оценивания составляющих градиента вследствие применения ПФП/ДФП;
2) высокая эффективность (скорость движения к экстремуму);
3) применение ПФП позволяет получить информацию о взаимодействии факторов, характеризующих кривизну поверхности отклика.
Недостаток:
1) сложность планирования пробных опытов, из-за применения ПФП/ДФП
2) меньшая оперативность по сравнению с симплексным методом.
4. Симплексный метод
Симплексомназывают выпуклую фигуру (или тело), образованную n+1 вершинами в пространстве n факторов (причем эти n+1 вершин не принадлежат одновременно ни одному из подпространств n-1 факторов). В случае одного фактора, симплексом служит отрезок, в случае двух факторов, - треугольник, при n=3 –тетраэдр, при n>4 привычным образом интерпретировать симплекс невозможно.
Симплексный метод позволяет совмещать пробные опыты (для определения направления движения) с рабочим движением по поверхности отклика к области оптимума. Основная идея симплексного метода состоит в следующем: если во всех n+1 вершинах симплекса поставить опыты и измерить отклик, то по величине отклика в вершинах можно судить, в каком направлении следует двигаться, чтобы приблизиться к экстремуму.
Метод рассмотрим на примере двухфакторного пространства (рисунок).
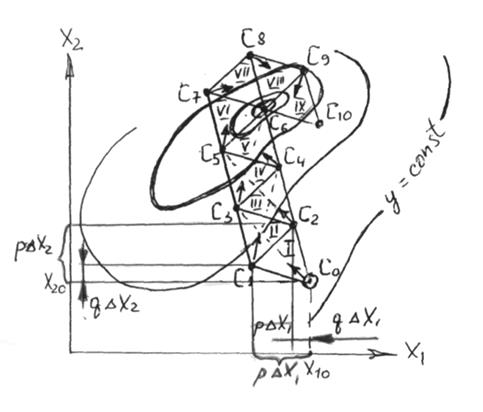
Последовательность метода.
4.1 Выбор начальной точки С0 (методика выбора одинакова для всех методов).
4.2 Выбор интервалов варьирования ∆xi по каждому фактору (методика выбора одинакова для всех методов).
4.3 Вычисление координат остальных вершин симплекса I.Для этого вычисляют безразмерные относительные величины p и q:
, 
.
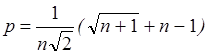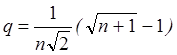Тогда остальные точки симплекса будут иметь координаты: С1 (x10±p∆x1; x20±q∆x2), C2(x10±q∆x1; x20±p∆x2).
4.4 Измерение отклика y в вершинах симплекса I; сравнение и определение наименьшего y.
4.5 Продвижение к экстремуму осуществляют путем зеркального отражения вершины с минимальным значением отклика через противолежащую сторону симплекса. Новый симплекс строится на двух старых и одной новой (отраженной) вершине.
4.6 Измерение отклика y всего в одной новой отраженной точке (С3); сравнение откликов во всех вершинах нового симплекса и определение наименьшего y.
4.7 Продвижение к экстремуму по п.4.5 продолжается до тех пор, пока симплекс не совершит полный оборот вокруг одной из вершин.
Достоинства симплексного метода:
1) высокая помехоустойчивость;
2) высокая скорость выхода к области экстремума.
Недостатки:
1) относительно высокая сложность вычисления координат вершин симплекса;
2) метод не позволяет непосредственно получить математическое описание изучаемого участка поверхности отклика, как в методе Бокса-Уилсона;
3) в условиях пологих поверхностей отклика метод дает менее точное решение, чем метод крутого восхождения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.