Корреляционно-регрессионный анализ. Проверки, проводимые в корреляционно-регрессионном анализе, страница 2

Формула расчета r_yx для генеральной совокупности: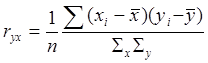

Формула расчета r_yx для выборки: 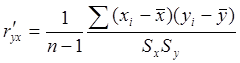, где

S_x, S_y – выборочные среднеквадратичные отклонения при большом объёме выборки .

Т.О. коэффициент корреляции – это количественная мера зависимости между изучаемыми величинами.

Коэффициент множественной корреляции рассчитывается на основе соответствующих коэффициентов парных корреляций. Например, для случая трёх переменных

,

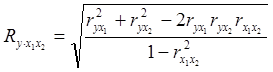где  - коэффициенты парных корреляций.

Свойства коэффициента корреляции

1. -1 £  r_yx £ +1
2.  Если r_yx > 0 – такая корреляция называется прямой (когда большему x соответствует большее y).
   Если r_yx < 0 – это обратная корреляция (большему x соответствует меньшее у).
3. Если r_yx = 0, следовательно, отсутствует линейная зависимость, но это не исключает существование нелинейной зависимости (например параболической  и т.д.).
4. Если r_yx = 1 – наличие линейной функциональной зависимости между x и y.
5. Чем теснее связь между переменными, тем ближе величина r_yx к +1 или -1.
   Введена такая градация:
   При | r_yx| = 0,3 – слабая корреляция
   0,3 £ | r_yx | £ 0,5 – умеренная
   0,5 £ | r_yx | £ 0,7 – заметная
   при | r_yx | > 0,7 – высокая степень тесноты связи.

3.            Аналитическая форма представления корреляционной зависимости осуществляется с помощью уравнения регрессии. В общем случае уравнение регрессии можно записать как y = f(x₁, x₂, ... x_n, a₀, a₁, ... a_m). (Т.о. мы переходим к регрессионному анализу.)

            Цель регрессионного анализа – аппроксимация неизвестной функции отклика известной математической моделью.

            Аппроксимация – это операция замены одной функции другой, в какой-то степени эквивалентной.

            В математической статистике при аппроксимации неизвестных функций отклика наиболее часто используют полиномиальные модели. Степень полинома определяется максимальной степенью входящих в него переменных. Например, для случая однофакторной задачи:

1.  полином нулевой степени: y = b₀ (1)

2.  полином первой степени: y = b₀ + b₁x (2)

3.  полином второй степени: y = b₀ + b₁x + b₁₁x² (3)

4.  полином третей степени: y = b₀ + b₁x + b₁₁x² + b₁₁₁x³ (4)

и т.д.

Первые два уравнения регрессии (уравнения вида (1) и (2)) будут линейными, остальные нелинейными.

Полиномиальная модель удобна, т.к. позволяет постепенно увеличивать степень точности аппроксимации за счет повышения порядка полинома.

На первом этапе корреляционно/регрессионного анализа используют линейные уравнения регрессии даже в случае исследования нелинейных корреляционных связей.

Рассмотрим два метода определения параметров уравнения регрессии на примере линейной однофакторной зависимости типа  y = b₀ + b₁x.

(1) Метод на основе коэффициента корреляции r_yx

            Зависимость между коррелируемыми параметрами x и y можно записать как

,

где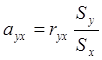

Подставив a_yx в уравнение и перенеся  в правую часть получим

.

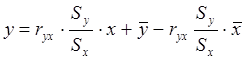Т.о. параметры b₀ и b₁ можно рассчитать по формулам:

,

,

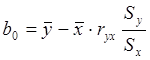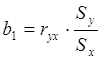где

; ; .

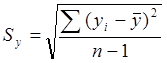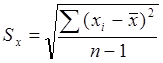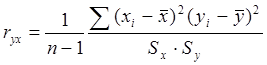(2) Метод наименьших квадратов (МНК)

            Сущность МНК заключается в определении коэффициентов регрессии (b₀, b_i),  которые бы обеспечивали минимум суммы квадратов отклонений экспериментальных данных (y_i) от значений, вычисленных по уравнению регрессии (y_i^p), т.е. минимум функции Д:

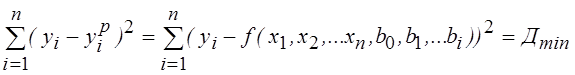
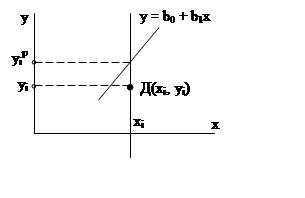
                                        Минимум любой функции,
                           распределение случайных величин которой
                           подчиняется закону Гаусса достигается при
                           одновременном равенстве нулю ее частных     
                           производных по всем неизвестным:

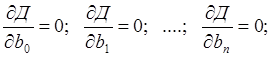
В результате такого дифференцирования получается система нормальных уравнений, когда число уравнений равно числу неизвестных коэффициентов.

Для рассматриваемой линейной однофакторной зависимости, когда
y = b₀ + b₁x, функция Д запишется как

.

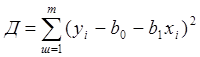После дифференцирования функции Д по ¶b₀ и ¶b₁ получаем систему из двух уравнений и двух неизвестных, решение которой дает следующие формулы для вычисления коэффициентов регрессии:

,

.

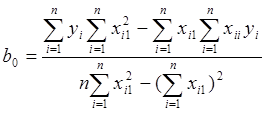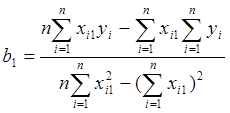Значение b_i.

По значению коэффициента регрессии можно судить о влиянии соответствующего фактора. Чем больше числовое значение коэффициента, тем большее влияние оказывает фактор на функцию отклика. Если коэффициент положителен, с повышением уровня фактора функции отклика увеличивается, и наоборот.