Корреляционно-регрессионный анализ. Проверки, проводимые в корреляционно-регрессионном анализе, страница 3

Вклад фактора в значение функции отклика, рассчитываемый как удвоенный коэффициент регрессии называется эффектом фактора.

Один из часто встречающихся видов нелинейности системы связан с тем, что эффект одного фактора зависит от уровня другого фактора. В этом случае говорят, что имеет место эффект взаимодействия факторов.

Эффект взаимодействия двух факторов называется эффектом первого порядка, трех факторов – второго порядка и т.д. Также применяются термины: парные эффекты взаимодействия факторов (x₁x₂, x₂x₃, ...); тройные (x₁x₂x₃, x₂x₃x₄, ...) и т.д.

Проверки, проводимые в корреляционно-регрессионном анализе.

Применение корреляционно-регрессионного анализа правомерно при соблюдении определенных условий. Решающими из них являются: (1) параметр оптимизации y есть случайная величина с нормальным законом распределения; (2) дисперсия y является однородной при различных наблюдениях y, что указывает на воспроизводимость экспериментов.

            Методы проверки соблюдения этих условий следующие:

I. Соответствие y нормальному закону распределения устанавливается с помощью критериев Пирсона и Колмогорова, (процедура проверки была рассмотрена ранее).

II. Воспроизводимость экспериментов (или однородность дисперсии) может оцениваться с помощью различных критериев:

II.1. При одинаковом числе экспериментов для каждой из дисперсий ряда используют критерий Кохрена: отношение максимальной дисперсии к сумме всех дисперсий ряда:

,

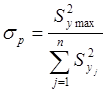n – число параллельных опытов или различных выборок. Дисперсии однородны, а эксперименты воспроизводимы при выполнении условия s_р < s_кр, (s_кр берется из соответствующих таблиц).

II.2. При неравном числе экспериментов для каждой из дисперсий ряда применяют критерий Бартлета (В). Расчет В приведен в специальной литературе.

Если дисперсии не однородны, необходимо: (1)выполнить преобразование y, приводящие к однородности (Например замена y на ln y); (2) устранить источники нестабильности эксперимента с помощью более точных методов и средств измерений.

III. Надежность (достоверность) коэффициента корреляции r_yx оценивается с помощью имеющей распределение Стьюдента статистики T_ka, которая вычисляется по формуле:

,

рассчитанная таким образом T_ka сравнивается с (T_ka)_кр, табулированным по a = 1 – р и k = n – 2, (р – вероятность, n – число опытов). Если расчетное значение T_ka больше найденного из таблиц (T_ka)_кр, то выборочный коэффициент корреляции r_yx надежен, т.е. переменные x и y являются коррелированными для всей генеральной совокупности.

IV. Значимость коэффициентов регрессии b_i может оцениваться сравнением абсолютного значения коэффициента |b_i| с доверительным интервалом Db_i. Доверительный интервал Db_i вычисляют по формуле:

Db_i = ± t_ТS_bi,

            где t_T – табличное значение критерия Стьюдента для принятого      уровня значимости a и числа степеней свободы, при которых определялось S_bi; S_bi – среднее квадратическое отклонение b_i, рассчитываемое по формуле:

,

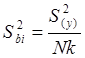 – дисперсия воспроизводимости эксперимента,

N – общее число опытов в матрице плана,

k – число параллельных опытов.

,

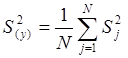 - дисперсии результатов реализации матрицы плана

N – число опытов или число строк матрицы плана.

            Коэффициент регрессии значим если |b_i| ³Db_i. Статистически незначимые коэффициенты могут быть исключены из уравнения регрессии.

            Незначимость некоторых коэффициентов может быть обусловлена (1) включением факторов, не влияющих на параметр оптимизации; (2) большой ошибкой в результатах опыта; (3) неудачным планированием эксперимента (а именно неудачным выбором интервалов варирования уровней факторов).

            V. Адекватность (соответствие) полученной зависимости (уравнения регрессии) экспериментальным данным проверяется по результатам расчета критерия Фишера (F_p) и сравнивая его с табличным значением (F_табл).

,

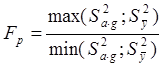В числителе находится большая, а в знаменателе – меньшая из оценок дисперсии.

S²_a×g – Оценка дисперсии адекватности, рассчитываемая по формуле:

,

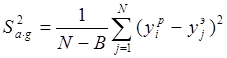где В – число коэффициентов уравнения регрессии;

       y_j^p и y_j^э – экспериментальное и расчетное (вычисленное по уравнению регрессии для условий j-го опыта) значения параметра оптимизации;

        - оценка дисперсии среднего значения параметра оптимизации, рассчитываемая по формуле:

.

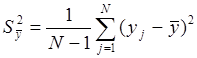            Если F_p < F_табл, уравнение регрессии считается адекватным экспериментальным данным. В случае неадекватности модели рекомендуется повысить степень полинома и произвести перерасчет.