Обобщающие показатели: интерпретация типических значений и перцентилей
В сложных ситуациях один из самых эффективных способов "увидеть всю картину" заключается в обобщении,т.е. использовании одного или нескольких отобранных или рассчитанных значений для характеристики набора данных. Подробное изучение каждого отдельного случая само по себе не является статистической деятельностью (если есть время для изучения каждого значения, может быть, это стоит сделать!), но обнаружение и идентификация особенностей, которые в целом характерны для рассматриваемых случаев, представляют собой статистическую деятельность, так как вся информация при этом рассматривается в целом.
Одна из целей статистики состоит в том, чтобы свести набор данных к одному числу (или двум, или нескольким), которое выражает наиболее фундаментальные свойства данных. Методы, наиболее подходящие для анализа одного списка чисел (т.е. одномерного набора данных), включают определение следующих показателей.
Среднее, медиана и мода— это различные способы выбора единственного числа, которое лучше всего описывает все числа в наборе данных. Такой представленный одним числом показатель называется типическим значением, или центром (также используют термин мера центральной тенденции).
Перцентиль (также используют термин процентиль) обобщает информацию о рангах, характеризуя значение, достигаемое заданным процентом общего количества данных, после того, как данные упорядочиваются (ранжируются) по возрастанию.
Стандартное отклонение— характеристика различий между значениями в наборе данных. Это понятие также называют разбросом, или изменчивостью.
Как быть, если набор данных содержит отдельные значения, которые неадекватно описываются этими показателями? Такие выбросы (сильно отклоняющиеся значения) можно просто описать отдельно. Таким образом, можно охарактеризовать большой набор данных, обобщив основные свойства большинства его элементов и затем создав список исключений. Это позволяет достичь статистической цели эффективного описания большого набора данных с учетом особой природы отдельных элементов.
4.1. Чему равно наиболее типическое значение?
Простейшее обобщение любого набора данных представляет собой единственное число, которое наилучшим образом представляет все значения данных. Такое число можно было бы назвать типическим значением для данного набора данных. Если не все значения в наборе данных одинаковы, то мнения о "наиболее типическом" могут быть разными. Существуют три вида такой обобщающей меры.
1. Среднее, которое можно вычислять только для имеющих содержательный смысл чисел (для количественных данных).
2. Медиана, или серединная точка, которую можно вычислять как для упорядоченных категорий (порядковые данные), так и для чисел.
3. Мода, или наиболее часто встречающаяся категория, которую можно вычислять для неупорядоченных категорий (для номинальных данных), для упорядоченных категорий и для чисел.
Среднее: типическое значение для количественных данных
Среднее чаще всего используют как типическое значение списка чисел и вычисляют путем сложения всех чисел списка и деления полученной суммы на количество чисел в списке (количество элементарных единиц). Формула вычисления выборочного среднего (т.е. среднего выборки данных) имеет следующий вид:
|
Выборочное среднее |
= |
Сумма значений элементов данных |
|
Количество элементов данных |
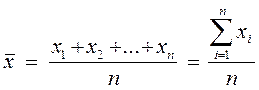
где п - общее число элементов в списке данных,
х1 ... хk ,— непосредственно сами значения данных.
Греческая прописная буква сигма, S, указывает на необходимость сложить все значения, которые записаны за ней, заменяя при этом индекс i значениями от 1 до п .
Понятие среднего не зависит от того, представляет ваш список чисел всю генеральную совокупность или же репрезентативную выборку из большей совокупности. В то же время обозначения несколько различаются. Для всей генеральной совокупности количество элементов обозначают буквой N, а среднее - буквой m (греческая буква "мю"). Процесс вычисления среднего одинаков как для генеральной совокупности, так и для выборки.
Поскольку при вычислении среднего значения данные суммируют, ясно, что среднее нельзя вычислять для качественных данных (нельзя складывать цвета или рейтинги долговых обязательств).
Среднее можно интерпретировать как равномерное распределение суммы всех значений между элементарными единицами. Таким образом, если каждое значение данных заменить средним, то общая сумма не изменится. Например, из базы данных служащих можно вычислить среднюю заработную плату служащих в Хьюстоне. Это среднее можно интерпретировать таким образом: если бы мы выплачивали всем служащим Хьюстона одинаковую заработную плату, не изменяя при этом общий фонд заработной платы, то значение этой заработной платы было бы равно среднему. Обратите внимание, что не следует рассматривать структуру уровня заработной платы, которая получена исходя из среднего, в качестве индикатора типичной заработной платы (особенно, когда вы имеете дело с фондом заработной платы как части бюджета).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.