Обобщающие показатели: интерпретация типических значений и перцентилей, страница 2

Поскольку среднее сохраняет неизменной сумму при равномерном распределе­нии значений, оно наиболее полезно в качестве обобщающего показателя при от­сутствии экстремальных значений (выбросов), когда набор данных представляет собой более-менее однородную группу с элементами случайности. Если один слу­жащий зарабатывает намного больше других, то среднее нельзя использовать в ка­честве обобщающего показателя. Хотя среднее и сохраняет неизменной общую сумму заработной платы, оно не будет хорошим показателем величины заработной платы отдельных служащих, так как среднее будет слишком высоким для боль­шинства служащих и слишком низким для этого высокооплачиваемого работника.

Среднее является только обобщающей характеристикой, которая сохраняет общую сумму. Это свойство среднего особенно полезно в тех ситуациях, когда необходимо планировать общую сумму для большой группы. Сначала вычисляют среднее для меньшей выборки данных, представляющей большую группу. Затем полученное среднее можно умножить на количество отдельных элементов в этой большей группе. В результате получают оценку или прогноз суммы для большей по размеру совокупности. В целом, если необходимо определить общую сумму, можно использовать среднее.

Пример. Сколько денег потратят потребители?

Фирма интересуется, сколько в целом тратят на медицинские товары жители Кливленда. Анализ случай­ной выборки из трехсот человек, живущих в данном регионе, показал, что в прошлом месяце каждый из них потратил в среднем $6,58. Естественно, кто-то потратил больше, а кто-то меньше этого среднего количества денег. Вместо того что­бы работать со всеми 300 числами, мы используем среднее, чтобы определить типическое значение ин­дивидуальных расходов каждого потребителя. Что особенно важно, умножив среднее значение расхо­дов на численность населения Кливленда, мы получили приемлемую оценку суммарных расходов на ме­дицинские товары жителей всего города:

Оценка затрат на медицинские товары жителей Кливленда = (среднее значение расходов одного чело­века из выборки) * (численность населения Кливленда) = ($6,58) * (503 000) = $3 309 740.

Этот прогноз суммарных продаж, равный $3 300 000, является приемлемым и, вероятно, полезным. Од­нако это значение не является точным (в том смысле, что оно не отражает точную сумму потраченных де­нег). Далее, при изучении доверительных интервалов, вы узнаете, как учитывать статистиче­скую ошибку, возникающую при распространении результата, полученного для выборки из 300 человек, на все население, состоящее из 503 000 человек.

Пример. Сколько имеется бракованных деталей?

Каждая партия изделий компании Globular Ball Bearing Company содержит 1000 изделий. Для проведе­ния контроля качества изделий из произведенных за день 253 партий была взята случайным образом выборка, включающая 10 партий. Число бракованных изделий в каждой партии составило:

3, 8, 2, 5, 0, 7, 14, 7, 4, 1

Среднее для этого набора данных:

3+8+2+5+0+7+14+7+4+1 / 10 = 5,1

демонстрирует, что в среднем каждая партия содержит 5,1 бракованных изделий. Иными словами, уро­вень брака составляет 5,1 изделия на 1000, или 0,51% (примерно полпроцента). Если распространить полученное среднее на все выпущенные за день 253 партии, то можно ожидать

5,1 * 253= 1290,3

бракованных изделий в дневном выпуске продукции, который составляет 253 000 изделий.

Чтобы показать, насколько среднее действительно является приемлемой обобщающей характеристикой списка чисел, на рис. 4.1.1 приведена гистограмма для этого набора данных из 10 чисел с обозначенным средним.

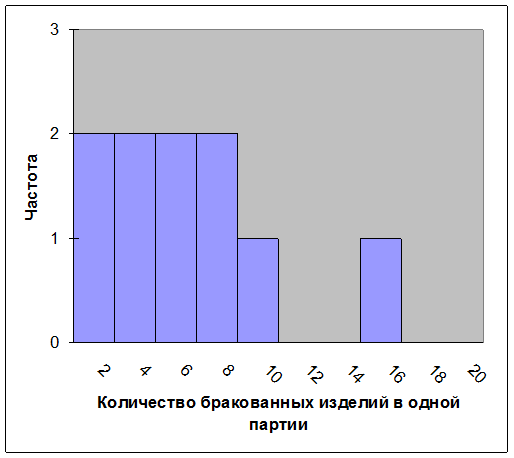
Рис. 4.1.1. Гистограмма количества бракован­ных деталей в каждой из 10 партий (од­на партия содержит 1000 изделий) с указанным средним значением (5,1)

Обратите внимание, насколько хорошо в середине данных расположено среднее, оно доста­точно близко ко всем значениям данных.

Взвешенное среднее: учет важности

Взвешенное среднее (используют также термин средневзвешенное) похоже на среднее, но позволяет присвоить различную важность (значи­мость), или "вес", каждому элементу данных. Взвешенное среднее дает возмож­ность гибко определять систему важности отдельных элементов данных в том случае, когда их нельзя рассматривать как равноценные.