Машиностроение \ Детали машин

Соединение деталей с натягом (прессовые соединения), страница 5

Практика использования соединений с натягом показывает, что небольшие пластические деформации на внутренней поверхности втулки не снижают в целом надежной работы соединения.

Что касается расчетного давления , то оно должно быть принято наибольшим, из возможных значений, реализуемых для данной посадки и данного диапазона изменения температуры окружающей среды. Это давление соответствует наибольшему из возможных натягов:

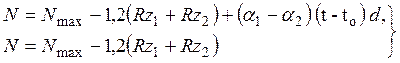(17)

Что касается прочности охватываемой детали (вала), то она может быть оценена лишь на основе комплексного учета всех нагрузок, действующих на эту деталь, в том числе со стороны втулки. Однако эта задача является чрезвычайно сложной. В связи с этим влияние насаженной на вал втулки в расчетной практике учитывают лишь косвенно, путем введения в расчеты эффективных коэффициентов концентрации напряжения . Так, например, рассчитывают на кручение и изгиб валы с посаженными на них с натягом зубчатыми колесами, шкивами ременных передач, муфтами и т.д.

Численное значение эффективного коэффициента концентрации зависит от многих факторов, в том числе от механических характеристик прочности материала вала, конструкции соединения, размеров деталей соединения посадочного давления, характера изменения напряжений в сечениях вала. Его численные значения могут доходить до 2 и выше.

Отметим, что у конструкторов имеются большие возможности снижения эффекта концентрации напряжения, в первую очередь, за счет выбора правильной формы вала и втулки (рис. 8).

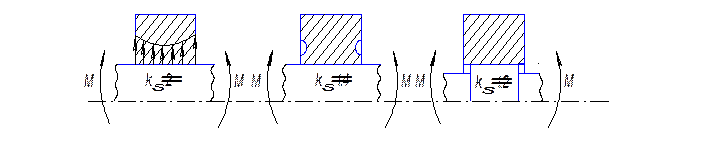
Рис. 8. Примеры конструктивного улучшения

формы деталей соединений с натягом

7. Примеры решения задач

Пример 1.В конструкции, представленной на рис. 9 а, бронзовая втулка 1 установлена в стальной корпус 2 опоры подшипника по посадке Н7/t6. Температура сборки . Проанализируйте, допустимо ли использовать такую конструкцию опоры при температуре окружающей среды , если минимально допустимое давление на посадочных поверхностях корпуса и втулки (при меньших давлениях возможно смещение втулки по отношению к корпусу под действием сил со стороны вала). Параметры шероховатости поверхностей – . Необходимые для расчета константы материала:

Бронза – модуль упругости , коэффициент Пуассона , коэффициент линейного расширения ;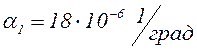

Сталь – модуль упругости , коэффициент Пуассона , коэффициент линейного расширения .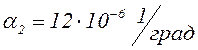

Решение.

1. Коэффициенты радиальной податливости втулки и корпуса подшипника находим, моделируя (см. рис. 9) охватывающую деталь (корпус) в виде цилиндра с внутренним диаметром и наружным диаметром :

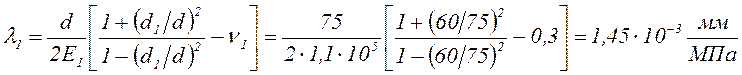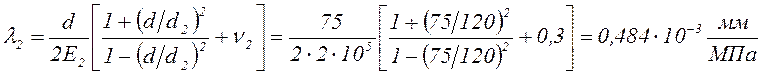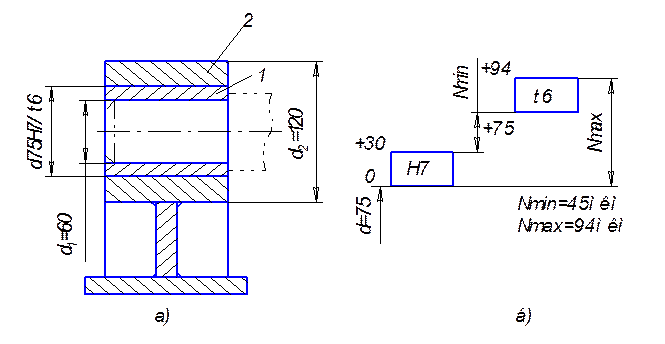
Рис. 9. Конструкция соединения с натягом (а) и схема

к определению натяга посадки (б)

2. Минимально допускаемый натяг, исходя из обеспечения прочности соединения:

3. Минимальное значение (возможного по условиям изготовления) натяга деталей соединения при заданной посадке H7/t6 (рис. 9б) с учетом влияния температуры окружающей среды, а также обмятия и среза микронеровностей в процессе запрессовки:

4. Сопоставляя значения и , приходим к заключению, что минимальный возможный натяг деталей соединения меньше минимального допустимого натяга, т.е. или, что то же самое, .

Если допустить, что минимальный натяг посадки H7/t6 для номинального диаметра равен (см. табл. 1), то с вероятностью 0,9986 условие () выполняется, поскольку в этом случае , т.е. на 7 мкм больше ().

Заключение. При использовании посадки H7/t6 условие прочности соединения не выполняется со 100-процентной вероятностью, но определенно выполняется с вероятностью 99,86%.

Пример 2. Проверить работоспособность соединения венца червячного колеса 2 со ступицей 1 (рис. 10), а также определить необходимую силу запрессовки при следующих исходных данных:

допускаемый коэффициент запаса по сцеплению ;

передаваемый вращающий момент ,

осевая составляющая усилия в зацеплении ;

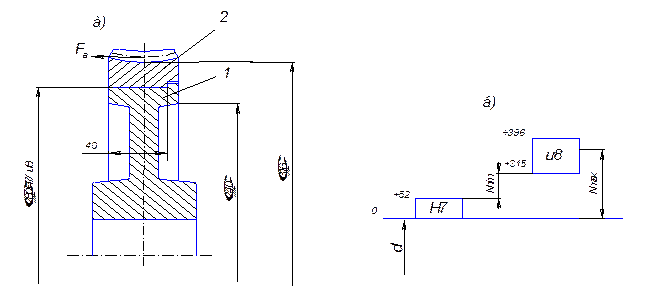
Рис. 10. Конструкция соединения с натягом (а) и схема

к определению предельных натягов посадки

материал ступицы – сталь 40Л (модуль упругости , коэффициент линейного расширения , коэффициент Пуассона ); материал венца – бронза Бр 01ОФ1 (модуль упругости , коэффициент линейного расширения , коэффициент Пуассона , предел текучести ); параметры шероховатости поверхностей – ; сборка венца со ступицей осуществлена способом запрессовки при температуре ; реализуемый на контактирующих поверхностях венца и ступицы коэффициент трения лежит в пределах ; диапазон изменения рабочей температуры червячного колеса , температура хранения червячного колеса .