Соединение деталей с натягом (прессовые соединения), страница 4

В инженерной практике пользуются упрощенными расчетами соединений с натягом, полагая, что после сборки деталей соединения давление на всей посадочной поверхности распределено равномерно, а реализуемые на этих поверхностях элементарные силы трения (сцепления) при нагружении соединения внешними силами, пропорциональны давлению и коэффициенту трения, зависящему лишь от способа сборки. Принятые допущения позволяют при расчете соединений цилиндрической и конической формы воспользоваться для установления связи между натягом и давлением на посадочных поверхностях известным решением задачи о сопряжении с натягом двух толстостенных цилиндров бесконечной длины (задача Ляме), не учитывать изменение коэффициента трения вдоль направления вектора относительно перемещения деталей соединения при сборке запрессовкой. Кроме того, в инженерных расчетах при оценке прочности деталей не учитывают напряжения, обусловленные рабочей  нагрузкой и центробежными силами.

Оценка прочности соединения. Обобщенная модель нагружения цилиндрического соединения с натягом представлена на рис. 7 а. Внешние нагрузки  и , размеры деталей соединения, тип посадки, а также физические контакты материалов деталей 1 и 2 (модули упругости, коэффициенты линейного расширения и др.) считаются известными. Требуется оценить прочность соединения (прочность связи).

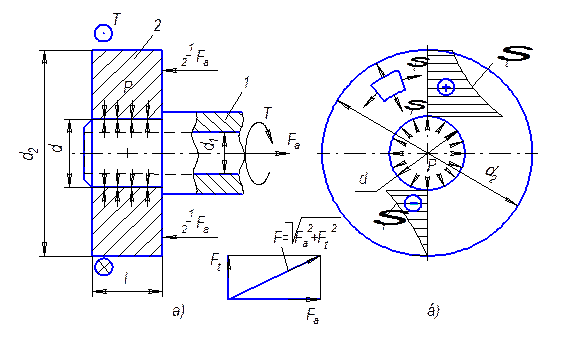
Рис. 7. Схема к оценке прочности соединения (а) и

прочности детали соединения – втулки (б)

Рассмотрим последовательно возможные варианты нагружения соединения.

1.  Положим, что   .

Тогда условие прочности соединения, состоящее в том, что вызываемая давлением  сила трения  должна быть больше внешней осевой силы  запишется следующим образом:

 или ,

где  – коэффициент запаса по сцеплению ().

Откуда 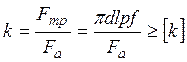                                                                    (10)

Здесь  – коэффициент трения пары вал – втулка,

 – нормативный (допускаемый) коэффициент запаса по сцеплению ().

2.  Пусть теперь ,  .

Условие прочности соединения (момент сил трения  должен быть больше внешнего момента Т):

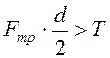,  или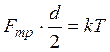

Здесь  – окружная сила трения.

Условие прочности соединения:

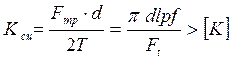                                                                          (11)

3.  Наконец ,  В данном случае действие момента  и осевой силы  целесообразно заменить эквивалентной им равнодействующей силой 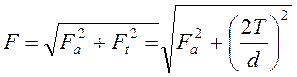(см. рис.).

Условие прочности соединения:

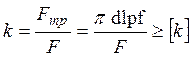.                                                                           (12)

Значение  в формулах (10), (11) и (12) определяется зависимостью (3). В качестве расчетного значения натяга для рассматриваемого случая следует принимать наименьшее из возможных его значений, принимая во внимание возможное обмятие поверхностей при сборке запрессовкой и влияние температуры окружающей среды. Поскольку в процессе работы соединения температурные деформации деталей могут, как уже указывалось ранее, приводить как к увеличению, так и уменьшению натяга по сравнению с исходными (состояние сборки), то в качестве расчетного натяга при детерминированном подходе следует принимать наименьшее из следующих двух значений:

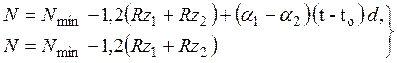                                    (13)

При вероятностном расчете в (13)  следует заменить на .

Что касается коэффициента трения в формулах (10), (11) и (12), то его численное значение также следует принимать наименьшим из возможных для рассматриваемых пар трения. В случае, когда перед сборкой соединения натяг контролируется (замеряется), то в формуле (13) вместо  следует подставлять измеренное значение натяга.

Оценка прочности деталей соединения.  В подавляющем большинстве практических случаев «слабым звеном» в отношении прочности является охватывающая деталь – втулка (рис. 7 б). Её обычно и рассчитывают на прочность, пользуясь результатами решения задачи об исследовании напряженного состояния толстостенного цилиндра с равномерным внутренним давлением (задача Ляме).

Анализ результатов решения этой задачи показывает, что наибольшие окружные () и радиальные () напряжения возникают на внутренней поверхности цилиндра. Эти напряжения определяются следующими формулами:

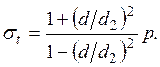                                                                            (14)

Эквивалентное напряжение на внутренней поверхности цилиндра

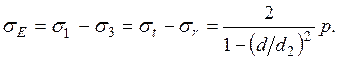                                                            (15)

Условие прочности детали 2 (втулки):

                                                                                                     (16)

где допускаемое напряжение для материала втулки .