Механика \ Вычислительная механика

Исследование влияния густоты конечно-элементной сетки и порядка аппроксимации конечного элемента на точность численного решения

Страницы работы

7 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Санкт-Петербургский государственный политехнический университет

Кафедра “Компьютерные технологии в машиностроении”

Отчёт

по лабораторной работе

Дисциплина: Вычислительная механика

Тема: Задача Ламе

Студенты гр. 3041/1 Додонов С.С., Емельянов А.С.

Преподаватель Елисеев К.В,

<<___>>_______________ 20__г.

Санкт-Петербург

2012 г.

Задание

Исследовать влияние густоты конечно-элементной сетки и порядка аппроксимации конечного элемента на точность численного решения.

Таблица 1

Вариант	2
Внутренний радиус, R₁	2,2
Внешний радиус, R₂	3,4
Давление, P	20000 Па
Модуль Юнга	2∙10¹¹
Коэффициент Пуассона	0,3

Характерный размер элемента 1/5 толщины стенки для грубой сетки. Для мелкой – в 2 раза меньше.

Теоретическая часть

Рассматривается бесконечно длинная прямая трубка, нагруженная постоянным внутренним давлением p. Наружная поверхность трубы свободна от действия нагрузки. Считается, что труба не растягивается вдоль своей оси, то есть находится в условиях плоской деформации. Внутренний радиус трубы равен R₁, внешний - R₂. Требуется найти окружные и радиальные напряжения в стенке трубы.

Точное решение задачи было найдено Г. Ламе. Напряжения σ_r (радиальная компонента) и σ_φ (окружная компонента) определяются по формулам:

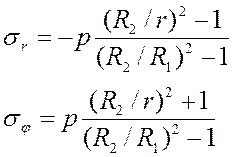
При малой толщине h=R₂ + R₁ стенки трубы по сравнению с её средним радиусом R=(R₂ + R₁)/2 наиболее опасной становится компонента σ_φ.В то время как σ_r монотонно изменяется от –p на внутренней стенке до нуля на внешней, σ_φ остается примерно постоянным и имеет значительно большую величину:

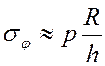
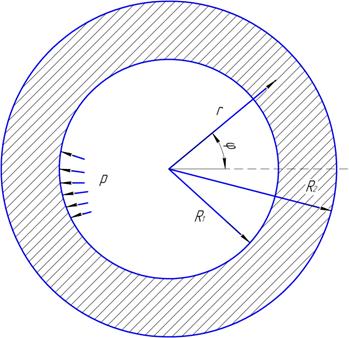
Рис.1. Сечение трубы

Выполнение работы

В табл. 2 представлены результаты решения в программе ANSYS на четырех разных конечно-элементных сетках для σ_r_.

Таблица 2

Грубая сетка элементов PLANE42		Мелкая сетка элементов PLANE42		Грубая сетка элементов PLANE82		Мелкая сетка элементов PLANE82
r	Ϭr	r	Ϭr	r	Ϭr	r	Ϭr
0	-1645,8	0	-1817,8	0	-1987,8	0	-1996,7
0,06	-1577	0,06	-1737,7	0,06	-1827,6	0,06	-1823,5
0,12	-1508,1	0,12	-1657,7	0,12	-1667,4	0,12	-1650,4
0,18	-1439,3	0,18	-1508,8	0,18	-1507,2	0,18	-1502,3
0,24	-1370,5	0,24	-1359,9	0,24	-1347	0,24	-1354,2
0,3	-1249,5	0,3	-1231,5	0,3	-1228,3	0,3	-1226,4
0,36	-1128,5	0,36	-1103	0,36	-1109,6	0,36	-1098,6
0,42	-1007,5	0,42	-991,53	0,42	-990,84	0,42	-987,6
0,48	-886,52	0,48	-880,02	0,48	-872,11	0,48	-876,56
0,54	-794,35	0,54	-782,56	0,54	-781,3	0,54	-779,48
0,6	-702,18	0,6	-685,11	0,6	-690,48	0,6	-682,4
0,66	-610,01	0,66	-599,44	0,66	-599,67	0,66	-597,02
0,72	-517,84	0,72	-513,78	0,72	-508,85	0,72	-511,64
0,78	-446	0,78	-438,07	0,78	-437,85	0,78	-436,17
0,84	-374,16	0,84	-362,37	0,84	-366,85	0,84	-360,69
0,9	-302,31	0,9	-295,14	0,9	-295,84	0,9	-293,64
0,96	-230,47	0,96	-227,9	0,96	-224,84	0,96	-226,59
1,02	-198,84	1,02	-167,93	1,02	-168,19	1,02	-166,75
1,08	-167,21	1,08	-107,95	1,08	-111,53	1,08	-106,92
1,14	-135,58	1,14	-79,65	1,14	-54,88	1,14	-53,278
1,2	-103,95	1,2	-51,348	1,2	1,7726	1,2	0,36227