Исследование влияния густоты конечно-элементной сетки и порядка аппроксимации конечного элемента на точность численного решения, страница 2

Грубая сетка элементов PLANE42		Мелкая сетка элементов PLANE42		Грубая сетка элементов PLANE82		Мелкая сетка элементов PLANE82
r	Ϭf	r	Ϭf	r	Ϭf	r	Ϭf
0	4995,2	0	4949,1	0	4868,8	0	4877,6
0,06	4796,7	0,06	4736,3	0,06	4708,6	0,06	4704,5
0,12	4598,2	0,12	4523,5	0,12	4548,4	0,12	4531,3
0,18	4399,7	0,18	4375,9	0,18	4388,2	0,18	4383,3
0,24	4201,2	0,24	4228,3	0,24	4228	0,24	4235,2
0,3	4083,9	0,3	4100,9	0,3	4109,3	0,3	4107,4
0,36	3966,7	0,36	3973,6	0,36	3990,5	0,36	3979,6
0,42	3849,4	0,42	3862,9	0,42	3871,8	0,42	3868,5
0,48	3732,1	0,48	3752,2	0,48	3753,1	0,48	3757,5
0,54	3642,3	0,54	3655,4	0,54	3662,2	0,54	3660,4
0,6	3552,5	0,6	3558,6	0,6	3571,4	0,6	3563,3
0,66	3462,7	0,66	3473,4	0,66	3480,6	0,66	3478
0,72	3372,9	0,72	3388,3	0,72	3389,8	0,72	3392,6
0,78	3302,6	0,78	3313	0,78	3318,8	0,78	3317,1
0,84	3232,3	0,84	3237,7	0,84	3247,8	0,84	3241,6
0,9	3162,1	0,9	3170,8	0,9	3176,8	0,9	3174,6
0,96	3091,8	0,96	3104	0,96	3105,8	0,96	3107,5
1,02	3024,7	1,02	3044,3	1,02	3049,1	1,02	3047,7
1,08	2957,7	1,08	2984,6	1,08	2992,5	1,08	2987,9
1,14	2890,6	1,14	2920,2	1,14	2935,8	1,14	2934,2
1,2	2823,6	1,2	2855,7	1,2	2879,2	1,2	2880,6

В табл. 4 приведены результаты точного решения по формулам Ламе для σ_r и σ_φ.

                                                                                                                                                                  Таблица 4

Точное решение
r	Ϭr точн	Ϭf точн
2,2	-2000	4880,952
2,26	-1819,74	4700,697
2,32	-1653,29	4534,246
2,38	-1499,27	4380,224
2,44	-1356,47	4237,423
2,5	-1223,83	4104,781
2,56	-1100,4	3981,355
2,62	-985,359	3866,312
2,68	-877,956	3758,908
2,74	-777,53	3658,483
2,8	-683,491	3564,444
2,86	-595,309	3476,261
2,92	-512,506	3393,458
2,98	-434,654	3315,606
3,04	-361,366	3242,318
3,1	-292,292	3173,245
3,16	-227,116	3108,068
3,22	-165,548	3046,501
3,28	-107,329	2988,281
3,34	-52,2185	2933,171
3,4	-8,32E-12	2880,952

Относительная погрешность :

грубая сетка PLANE42:

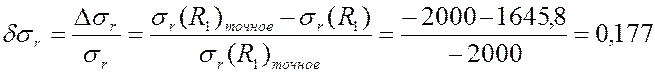
мелкая сетка PLANE42:

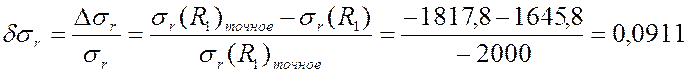
грубая сетка PLANE82:

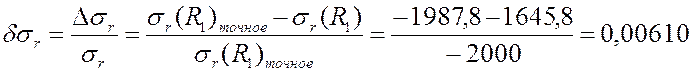
мелкая сетка PLANE82:

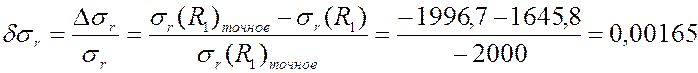
Относительная погрешность :

грубая сетка PLANE42:

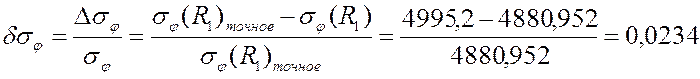
мелкая сетка PLANE42:

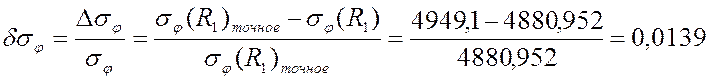
грубая сетка PLANE82:

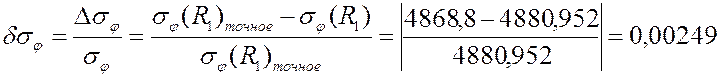
мелкая сетка PLANE82:

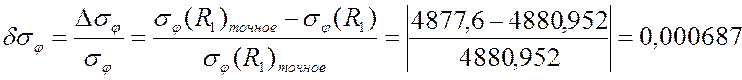
Относительная погрешность :

грубая сетка PLANE42:

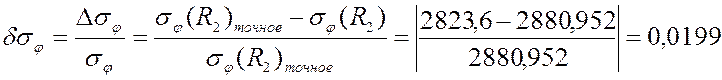
мелкая сетка PLANE42:

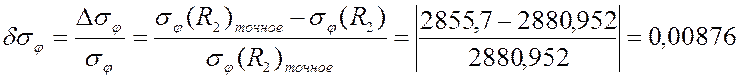
грубая сетка PLANE82:

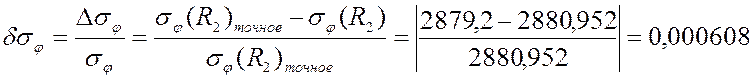
мелкая сетка PLANE82:

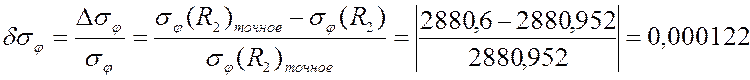
В табл. 5 приведены относительные погрешности, которые были рассчитаны выше, для 4-х вариантов расчетов в Ansys.

Таблица 5

На рис.1 показаны график σ_r(r)  точного решения и четыре графика σ_r(r), соответствующие четырем разным конечно-элементным сеткам (М1-грубая сетка, М2- мелкая сетка).

На рис.2 показаны график σ_φ(r)  точного решения и четыре графика σ_φ(r), соответствующие четырем разным конечно-элементным сеткам (М1-грубая сетка, М2- мелкая сетка).

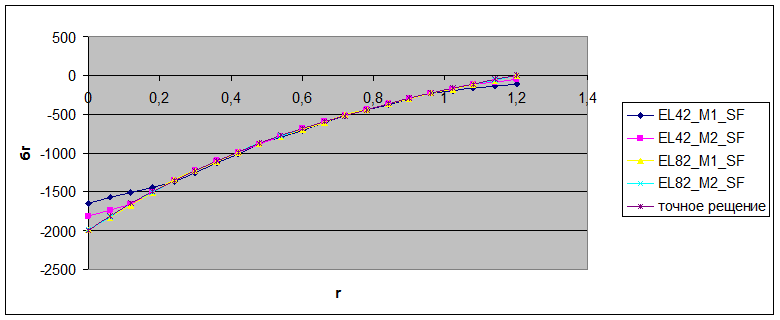
Рис.1. Графики зависимости радиального напряжения σ_r(r)

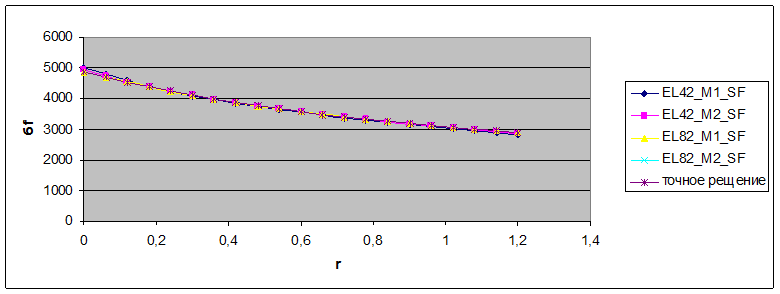
Рис.2. Графики зависимости радиального напряжения σ_φ(r) 

Вывод:

Точность численного решения возрастает с увеличением густоты и использованием элементов с квадратичной аппроксимацией. Так для грубой сетки элементов с линейной аппроксимацией PLANE42 относительная погрешность радиального напряжения и уменьшается с увеличением густоты сетки до 9,11%. При использовании же сетки элементов с квадратичная аппроксимацией PLANE82 эта погрешность значительно ниже и составляет 0,61% - для грубой сетки 0,165% - для мелкой сетки элементов. Аналогичная картина наблюдается и при вычислении окружного напряжения.