Применение общего уравнения динамики для силового расчета механизмов. Применение общего уравнения динамики для определения реакции в кинематической паре. Трение в кинематических парах

нулю работа сил реакций, действующих на каждое отдельное звено.

Если механизм имеет w степеней свободы и q₁,…,q_w – его обобщенные координаты, то

     (4.29)

Подставляя (4.29) в (4.28) и используя независимость вариаций обобщенных координат dq_S, получаем следующую систему уравнений:

. (4.30)

Для механизма с одной степенью подвижности система (4.30) сводится к одному уравнению

(4.31)

Поскольку в этом случае ,

где  – скорость точки 0_i, уравнение (4.31) записывается также в форме

 (4.32)

Отсюда следует, что сумма возможных мощностей всех активных сил и сил инерции в любой момент времени равна нулю для механизма с одной степенью подвижности при идеальных кинематических парах.

Определение движущих сил. Выделим обобщенные движущие силы из прочих активных сил, имеем

              (4.33), где  – главный вектор всех активных сил, приложенных к i–му звену, кроме движущих, а – главный момент этих сил.

получаем уравнения, аналогичные (4.30):

.       (4.34)

Пример: уравнение Даламбера-Лагранжа для кривошипно-ползунного механизма:

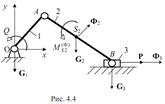
(4.36)

8. Применение общего уравнения динамики для определения реакции в кинематической паре.

Общее уравнение динамики позволяет определить реакции всех освобождающих связей. Определить реакцию R₀₃ в поступательной паре.

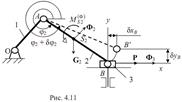Определим связь, соответствующую этой реакции. Координата y_B будет играть роль второй входной координаты, а реакция R₀₃ станет обобщенной «движущей» силой, соответствующей этой координате. Применим к этому механизму общее уравнение динамики:

При dq = 0, dy_B ¹ 0 работу будут совершать только силы, приложенные к звеньям 2 и 3:

(4.38)

Из геометрических соображений (см. рис.4.11) можно получить, что

(4.39)

Изложенный метод можно применить для определения реакции любой освобождающей связи. Что же касается неосвобождающих связей, то соответствующие им реакции в принципе невозможно определить в процессе силового расчета механизма.

10. Трение в кинематических парах. Трение скольжения, качения и верчения. Модель высшей КП с точечным контактом.

S – поверхность соприкосновения элементов кинематической пары.

Выделим на этой поверхности элементарную площадку dS  в окрестности некоторой точки A. Сила   называется силой трения скольжения; момент  – моментом трения качения, а момент  – моментом трения верчения. векторы  и  – противоположны по направлению соответственно касательной   и нормальной  составляющим вектора относительной угловой скорости. Закон Амонтона – Кулона:

     (5.1)

где f – безразмерный коэффициент трения скольжения, а k и k_В – коэффициенты трения качения и верчения.

(5.2)

Суммарная сила трения:  (5.3)

где S – поверхность соприкосновения. Для того чтобы воспользоваться этой формулой, нужно знать закон распределения нормальных реакций по поверхности  S.

Если скорость скольжения в точке контакта и относительная угловая скорость равны нулю, суммарные силы и моменты сил трения в

кинематической паре могут быть определены из условий равновесия звеньев.

F = P,   M_К = Pּr. (5.4)

Нарушение состояния покоя (качение):  (5.5)

где k – коэффициент трения качения, то начнется качение цилиндра по плоскости без скольжения. Скольжение начинается при нарушении условия  , (5.6), где f_n – коэффициент трения покоя, обычно несколько превышающий величину коэффициента трения скольжения f.

9. Силовой расчет механизмов, содержащих высшие кинематические пары. Расчет кулачкового механизма методом кинетостатики и с помощью общего уравнения динамики.

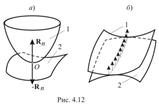При точечном контакте абсолютно твердых звеньев и при отсутствии сил трения реакции в кинематической паре сводятся к силе R_n, направленной по общей нормали к контактирующим поверхностям.

Такая пара является пятиподвижной, и в ней возникает одна неизвестная компонента реакции (рис.4.12, а). При линейном контакте силы взаимодействия (при отсутствии трения) распределены вдоль линии контакта и направлены в каждой точке по общей нормали к поверхностям (рис.4.12, б).

Рассмотрим некоторые примеры.

а). Расчет плоского кулачкового механизма. Рассмотрим кулачковый механизм, состоящий из кулачка 1 и поступательно движущегося толкателя 2 (рис.4.14).

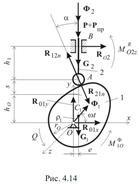Механизм содержит две низших кинематических пары (O и B) и одну высшую (A). В плоскости движения во вращательной паре две неизвестных компоненты реакции – R_01x и R_01y, в поступательной – R₀₂ и , и в высшей кинематической паре – нормальная сила R_12n= – R_21n. Вместе с обобщенной силой Q имеем шесть неизвестных. Для их отыскания можем составить шесть уравнений кинетостатики, которые