Определим массы противовесов и углы их установки для механизма рис.7.13, если длины звеньев и массы определяются выражениями:
ОА = АС2-= r, АВ = 2r, m=m1 = m2= m3.
Координаты точек A,B и их вторые производные по φ (аналоги ускорения):
![]()
![]()
![]()
Запишем выражение для первой гармоники главного вектора сил инерции (в xB'' оставляем только первое слагаемое):
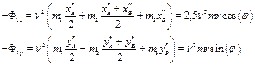
Учитывая, что масса механизма M=3m, из (6.16) получаем коэффициенты при ![]() :
:
![]() Принимаем
радиусы установки противовесов
Принимаем
радиусы установки противовесов ![]() . Из (7.28) определяем углы установки
противовесов и их массы:
. Из (7.28) определяем углы установки
противовесов и их массы:
![]()
Противовесы в этом случае оказываются менее громоздкими.
Чаще всего ограничиваются установкой одного противовеса,
уменьшающего первую гармонику неуравновешенной силы, но не обеспечивающего
полное ее устранение. Можно, например, минимизировать наибольшее значение модуля
![]() .
.
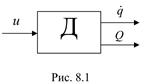 При решении задач
динамики машин обычно используют наиболее простые динамические модели
двигателей, отражающие зависимости между законами изменения во времени
входного параметра двигателя (управления) u(t) , обобщенной
координаты выходного звена q(t) и обобщенной движущей силы Q(t) (рис.8.1).
Математические соотношения, описывающие эти зависимости, называются механическими
характеристиками двигателей. К более сложным моделям, учитывающим динамику внутренних физических процессов, происходящих в двигателях, приходится
обращаться сравнительно редко; в этом курсе такие модели рассматриваться не
будут.
При решении задач
динамики машин обычно используют наиболее простые динамические модели
двигателей, отражающие зависимости между законами изменения во времени
входного параметра двигателя (управления) u(t) , обобщенной
координаты выходного звена q(t) и обобщенной движущей силы Q(t) (рис.8.1).
Математические соотношения, описывающие эти зависимости, называются механическими
характеристиками двигателей. К более сложным моделям, учитывающим динамику внутренних физических процессов, происходящих в двигателях, приходится
обращаться сравнительно редко; в этом курсе такие модели рассматриваться не
будут.
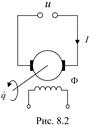 С основными разновидностями механических характеристик
познакомимся на примере электродвигателя постоянного тока с независимым
возбуждением, принципиальная схема которого показана на рис.8.2. Здесь
вращение выходного звена двигателя (ротора) происходит за счет взаимодействия
тока, возникающего в обмотке ротора, с магнитным полем, создаваемым обмоткой
возбуждения . При вращении ротора в его обмотке в соответствии с законом
электромагнитной индукции возникает обратная электродвижущая сила Е
(ЭДС) , пропорциональная величине магнитного потока обмотки возбуждения Ф и
угловой скорости ротора
С основными разновидностями механических характеристик
познакомимся на примере электродвигателя постоянного тока с независимым
возбуждением, принципиальная схема которого показана на рис.8.2. Здесь
вращение выходного звена двигателя (ротора) происходит за счет взаимодействия
тока, возникающего в обмотке ротора, с магнитным полем, создаваемым обмоткой
возбуждения . При вращении ротора в его обмотке в соответствии с законом
электромагнитной индукции возникает обратная электродвижущая сила Е
(ЭДС) , пропорциональная величине магнитного потока обмотки возбуждения Ф и
угловой скорости ротора ![]() :
: ![]() где kE– некоторый коэффициент пропорциональности. В
цепи ротора при прохождении тока I возникают потери напряжения,
связанные с наличием активного сопротивления R и индуктивности L
. С учетом потерь уравнение электрической цепи записывается в форме
где kE– некоторый коэффициент пропорциональности. В
цепи ротора при прохождении тока I возникают потери напряжения,
связанные с наличием активного сопротивления R и индуктивности L
. С учетом потерь уравнение электрической цепи записывается в форме
![]()
С другой стороны, в соответствии с законом Ампера движущий момент Q связан с силой тока I соотношением
![]() .
Исключая I из (8.1) и (8.2), получаем
.
Исключая I из (8.1) и (8.2), получаем
![]()
Обозначив ![]() , легко преобразовать это выpажeниe к виду
, легко преобразовать это выpажeниe к виду
![]()
Соотношение (8.4) , связывающее входной (u) и выходные (![]() ) параметры двигателя, называется динамической
характеристикой. Параметр τ называется электромагнитной
постоянной времени и характеризует инерционность электромагнитных процессов,
происходящих в двигателе. Обычно величина его лежит в пределах от 0,02 до 0,1
с. Параметр s называется крутизной
характеристики двигателя. Чем больше крутизна s, тем слабее изменение нагрузки влияет на величину
угловой скорости ротора. Характеристика (8.4) широко используется при
анализе динамических процессов, происходящих в машинах, приводимых в движение
электродвигателями постоянного тока с независимым возбуждением. Если
исследуется статический процесс, при котором Q=Const, выражение (8.4) упрощается и переходит в статическую
характеристику двигателя:
) параметры двигателя, называется динамической
характеристикой. Параметр τ называется электромагнитной
постоянной времени и характеризует инерционность электромагнитных процессов,
происходящих в двигателе. Обычно величина его лежит в пределах от 0,02 до 0,1
с. Параметр s называется крутизной
характеристики двигателя. Чем больше крутизна s, тем слабее изменение нагрузки влияет на величину
угловой скорости ротора. Характеристика (8.4) широко используется при
анализе динамических процессов, происходящих в машинах, приводимых в движение
электродвигателями постоянного тока с независимым возбуждением. Если
исследуется статический процесс, при котором Q=Const, выражение (8.4) упрощается и переходит в статическую
характеристику двигателя:![]()
Статическая характеристика может использоваться и для
исследования таких динамических процессов , при которых ![]() , то есть в тех случаях , когда
малой является либо постоянная времени τ, либо производная
, то есть в тех случаях , когда
малой является либо постоянная времени τ, либо производная ![]() .
.
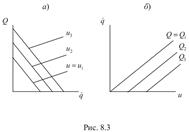 На рис.8.3 построены два семейства статических
характеристик: на рис.8.3,а изображены рабочие характеристики, выражающие зависимости
На рис.8.3 построены два семейства статических
характеристик: на рис.8.3,а изображены рабочие характеристики, выражающие зависимости ![]() при
различных постоянных значениях u; на
рис.8.3,б представлены регулировочные характеристики
при
различных постоянных значениях u; на
рис.8.3,б представлены регулировочные характеристики ![]() , построенные для различных
постоянных значений Q. В рассматриваемом
случае все эти характеристики являются линейными
, построенные для различных
постоянных значений Q. В рассматриваемом
случае все эти характеристики являются линейными
. Регулировочная характеристика, соответствующая Q = 0 ( то есть определяющая зависимость при отсутствии нагрузки на двигатель), называется характеристикой холостого хода. При определенных условиях эта характеристика может рассматриваться как приближенная и при Q≠0. Это имеет место в тех случаях, когда статическая характеристика двигателя является достаточно жесткой, то есть когда крутизна s достаточно велика, так что влиянием нагрузки на скорость можно в первом приближении пренебречь. Характеристика. полученная при таком предположении, называется идеальной кинематической характеристикой; она может быть приведена к виду
![]()
В соответствии с этой характеристикой угловая скорость ротора полностью определяется значением входного параметра двигателя: при ее использовании двигатель становится как бы "источником
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.