Изучение численного метода Эйлера решения ОДУ первого порядка

Санкт-Петербургский государственный политехнический университет

Отчёт

о лабораторной работе

Дисциплина: Вычислительная математика

Тема: Решение ОДУ первого порядка методом Эйлера

Вариант №7

Студент гр. 2041.2                                                  Тишков А.      

Преподаватель                                                         Щенёв В.В.       

                                                                         _____________ 2011 г.

Санкт-Петербург

2011

Лабораторная работа №10

Решение ОДУ первого порядка методом Эйлера

Цель работы – изучение численного метода Эйлера решения ОДУ первого порядка, приопретение навыков использования соответствующих численных методов с применением программных средств автоматизации вычислений.

Задание

Этапы:

1. Вычисление общих параметров
2. Метод Эйлера
3. Первый модифицированный метод Эйлера
4. Второй модифицированный метод Эйлера
5. Построение графиков полученных решений

Краткие теоретические сведения

Дифференциальные уравнение – такие уравнения, в которых неизвестными являются не переменные (т.е. числа), а функции одной или нескольких переменных.

Определение: Если в уравнения входят производные только по одной переменной, то они называются обыкновенными дифференциальными уравнениями (ОДУ).

ОДУ первого порядка записывается в виде: y’ = f(x,y)

Решением (интегралом) ОДУ называется всякая функция y = f(x), удовлетворяющая этому уравнению, т.е. такая, после подстановки которой в исходное уравнение оно обращается в тождество.

Общее решение записывается в виде: y = f(x) + const

Суть метода Эйлера заключается в том, что мы рассматриваем ОДУ первого порядка с некоторым начальным условием на отрезке [a,b]. Отрезок разбиваем на n равных частей, устанавливаем шаг интегрирования h = (b-a)/n. После этого строим график y от x. На графике мы получаем семейство кривых. Точным решением будет являться такая кривая, которая проходит через точку, соответствующую начальным условиям [x₀,y₀].

1.Вычисление общих параметров

2.Метод Эйлера

3.Первый модифицированный метод Эйлера

4.Второй модифицированный метод Эйлера

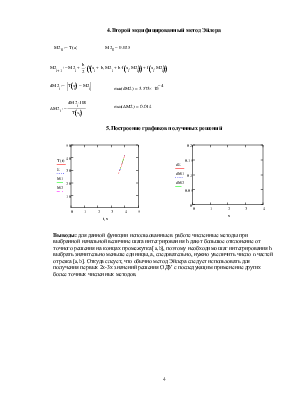
5.Построение графиков получнных решений

Выводы: для данной функции использованные в работе численные методы при выбранной начальной величине шага интегрирования h дают большое отклонение от точного решения на концах промежутка [a,b], поэтому необходимо шаг интегрирования h выбрать значительно меньше единицы, а, следовательно, нужно увеличить число n частей отрезка [a,b]. Откуда слеует, что обычно метод Эйлера следует использовать для получения первых 2х-3х значений решения ОДУ с последующим применение других более точных численных методов.