Изучение численного метода Рунге-Кутты для решения ОДУ первого порядка

11. Решение ОДУ методом Рунге-Кутты

11.1  Цель работы

Целью данной работы является изучение численного метода Рунге-Кутты  для  решения ОДУ первого порядка, приобретение навыков применения  программных средств автоматизации  вычислений.

11.2  Задание

Задание включает ОДУ, его точное решение и границы отрезка [a,b].

Варианты ОДУ взять из предыдущей работы, начальное значение y0 вычислить, пользуясь формулой точного решения.

11.3  Теоретические сведения

Общая идея вывода формулы метода Рунге-Кутты любого порядка состоит в следующем:

Пусть y(x) –решение дифференциального уравнения y¢(x)=f(x,y(x)), удовлетворяющее условию y(x_n)=y_n. Проинтегрируем уравнение y¢(x)=f(x,y) на промежутке по xÎ[x_n,x_n+1], получим: 

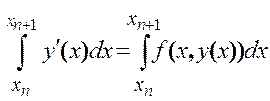                                                             (11.1)

по формуле Ньютона-Лейбница       .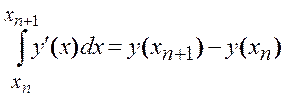      

Тогда 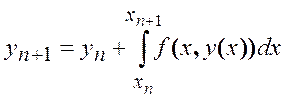                                                          (11.2)

Если бы интеграл в формуле вычислялся точно , то она была бы основной рабочей формулой всех методов численного интегрирования дифференциальных уравнений.

В действительности используют приближенную формулу , заменяя определенный интеграл квадратурной суммой.

На отрезке [x_n,x_n+1]  вводят m  вспомогательных узлов  , где 0=a₁£a₂£a₃£…£a_m£1 .

Тогда интеграл можно  заменить квадратурной суммой

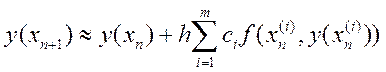                                      (11.3)             

Здесь неизвестны  . Применяя (11.2) , получим

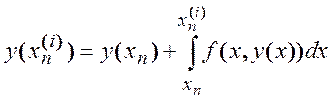                        , где     i=2,3,…,m

Выполнив необходимые преобразования , получим :

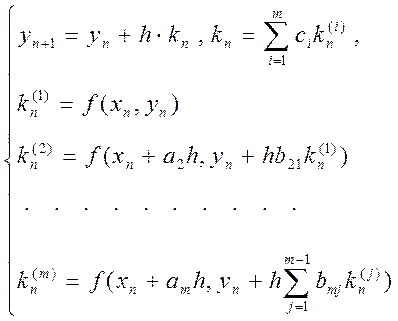                                            (11.4)

Выбор конкретных значений c_i, a_i  и  b_i осуществляется по-разному и дает ту или иную модификацию метода Рунге-Кутты. Приведем рабочие формулы метода четвертого порядка , который применяется настолько широко , что в литературе называется просто «методом Рунге-Кутты» без всяких указаний на тип или порядок. Ошибка метода e=O(h⁵) , при его использовании необходимо вычислять функцию четырежды.

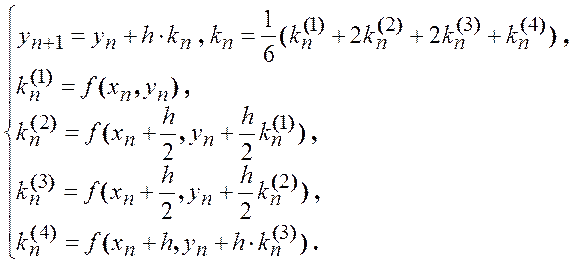                  (11.5)

Для оценки ошибки интегрирования также используется принцип Рунге .

Пусть есть точное решение ДУ при .

Тогда для метода Рунге-Кутты справедлива оценка погрешности

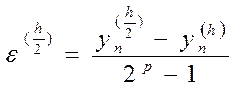
Здесь -   приближение к точному решению , вычисленное с шагом h/2 -  приближение , вычисленное с шагом h.

Для метода  p=4 , тогда ошибка интегрирования :

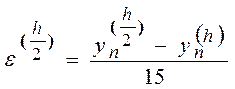
Предложено несколько полуэмпирических критериев смены шага и выбора оптимального шага интегрирования при условии достижения заданной точности.

Например , используется такое оценочное правило :

  если 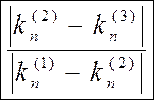  достаточно велико (больше нескольких сотых ), то шаг интегрирования необходимо уменьшить .

Для численного интегрирования ОДУ в Mathcad имеется выбор использовать встроенный вычислительный  блок  Given/Odesolve , либо встроенные функции rkfixed, Rkadapt  и другие в зависимости от используемого метода. Использование блока предпочтительнее из соображений наглядности, встроенные функции  дают пользователю больше рычагов воздействия на численные методы.

11.4  Порядок  выполнения  работы

·  Вариант ОДУ взять из работы 10.

·  Вычислить решение ОДУ 1-ым модифицированным методом Эйлера и методом Рунге-Кутта

·  Построить сравнительный график всех полученных решений  с  точным решением, указанным в задании.

·  Оценить ошибку полученного численного решения по методу Рунге-Кутты для выбранного шага  и проверить критерий выбора оптимального шага

·  Воспользоваться встроенными функциями Mathcad  для решения заданного ОДУ, построить графики

11.5  Пример выполнения задания

 ОДУ : 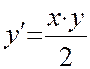  , интервал [0,4]  , точное решение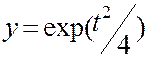 

1. Вычисление общих параметров