|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1-ый модифицированный метод Эйлера
|
|
|
Начальное значение функции |
|
|
|
|
2. Составим программу для вычисления решения по методу Рунге-Кутты
|
|
|
|
|
|
3. Графики точного решения T(t) , приближенного решения M1 и приближенного решения RK по методу Рунге-Кутты
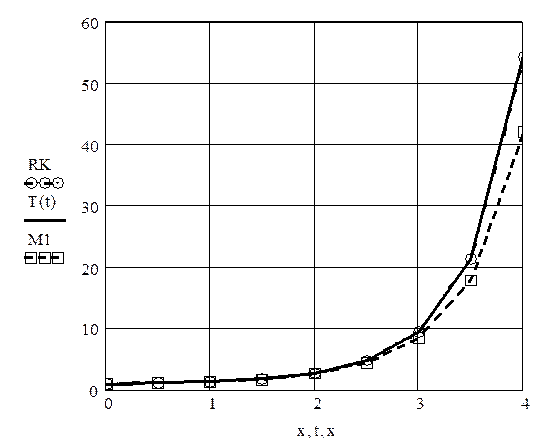
Рис.11.1
4. Оценка ошибки по методу Рунге при выбранном шаге h
Погрешность 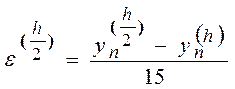
|
|
|
|
|
Увеличиваем величину шага и пересчитаем количество шагов Границы интервала Начальное значение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Восстанавливаем первоначальную величину шага и количество шагов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
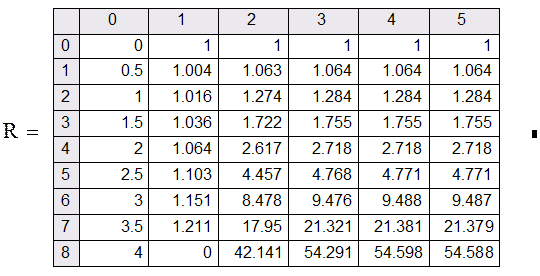
Погрешность по Рунге свидетельствует о том , что в любой точке значение функции , полученное при величине шага h/2 , отличается от точного не более, чем на max(ε).
5.Критерий выбора оптимального шага
|
|
|
|
|
|
|
|
|
|
|
|
Возьмем ![]()
![]()
6. Использование встроенных функций Mathcad
|
|
|
Начальное значение Встроенные функции с постоянным и переменным шагом интегрирования Переменная точного решения Создание совмещенной таблицы сравнения результатов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь рассмотрим применение блока Given-Odesolve
|
|
|
|
|
|
|
|
Уравнение записывается в стандартном виде относительно независимой переменной . Знак равенства взят из булевых операторов. Начальное значение численного решения должно быть указано перед командой Odesolve , в которой надо указать имя переменной, вторую границу интервала и количество шагов
Решение получим в виде таблицы значений или графика.
Точность блока Given-Odesolve 10-5.
11.6 Содержание отчета
1. Титульная страница с названием работы.
2. Задание.
3. Назначение работы и краткие теоретические сведения.
4. Расчет решения заданного ОДУ методом Рунге- Кутта, 1-м модифицированным Эйлера, совмещенный график полученных решений
5. Расчет ошибки интегрирования по методу Рунге
6. Выбор оптимального шага интегрирования по критерию max(O).
7. Получение численного решения уравнения встроенными функциями .
8. Выводы по результатам.
11.7 Контрольные вопросы
1. Суть метода Рунге-Кутта.
2. Графическая интерпретация коэффициентов Рунге-Кутта.
3. Ошибка метода Рунге-Кутта.
4. Правило Рунге по оценке ошибки интегрирования ОДУ.
5. Критерий выбора оптимального шага.
6. Применение встроенных функций rkfixed, Rkadapt .
7. Использование блока Given-Odesolve .
11.8 Литература
1. Демидович Б.П., Марон И.А., Основы вычислительной математики.- Москва, Наука,1970 г.-664 с.
2. Копченова Н.В., Марон И.А., Вычислительная математика в примерах и задачах.-М.,Наука,1972 г.-368 с.
3. Шапорев С.Д., Методы вычислительной математики их приложения-СПб, СМИО Пресс,2003 г.,-232с.
4. Кирьянов Д.В., самоучитель Mathcad 11.-СПб,БХВ Петербург,2003 г.
5. Плис А.И., Сливина Н.А., Mathcad : математический практикум.-М.: Финансы и статистика,1999.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.