Знакомство с методом Монте-Карло, как численным методом решения математических задач при помощи моделирования случайных величин

15. МЕТОД  МОНТЕ-КАРЛО

15.1 Цель   работы

          Целью работы является знакомство с методом Монте-Карло , как численным методом решения математических задач при помощи моделирования случайных величин.

15.2 Задания

Найти объем тела , заданного ограничивающими его поверхностями.

                                                                                                Таблица 15.1

№ п/п	поверхность  1	поверхность 2	поверхность 3	поверхность 4
1	у=16√2х	у=√2х	z=0	x+z=2
2	у=5√х	у=5∕3	z=0	z=5+5∕3√х
3	у=√х	x+у=2	z=0	z=12у
4	х=√у	х+у=2	z=0	z=12х∕5
5	у=√2х	х+у=4	z=0	z=3у
6	х=19√2у	х=4√2у	z=0	z+у=2
7	у=√3х	х+у=6	z=0	z=4у
8	х=√3у	х+у=6	z=0	z=4х/5
9	х=√2у	х=16√2у	z=0	z+у=2
10	х=2√2у	х=17√2у	z=0	z+у=0,5
11	у=√4у	х+у=8	z=0	z=3у
12	у=5∕3√х	у=5х/9	z=0	z=5/9(3+√х)

15.3 Теоретические сведения

В основе многих физических явлений , таких, как молекулярное движение, лежат случайные процессы. Их закономерности подтверждаются при большом количестве опытов, теоретически бесконечном. Любой статистический эксперимент может быть осуществлен не чисто физическими средствами, а средствами вычислительной техники. Кроме того, вместо решении аналитической задачи можно моделировать случайный процесс и использовать статистические оценки вероятностей и средних статистических данных или, так называемых, математических ожиданий и других моментов для приближенного решения данной аналитической задачи.

Подчеркнем особенности метода:

1)     простая структура вычислительного алгоритма,

2)    погрешность вычислений – чаще она пропорциональна , где D=const, N- число испытаний. Из неравенства Чебышева видим, что в зависимости от требуемой точности ε следует провести  N испытаний:

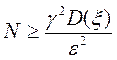 , где γ находится из соотношения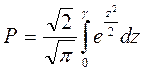

Если  P- заданное значение вероятности , то :

P=0,9    →   γ=0,1736

P=0,99  →   γ=0,1897

P=0,999 →  γ=0,1914

Например : для Р = 0,99 и  ε=10^-3  можно найти N при D=1∕12.

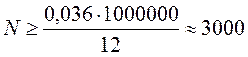
                    Метод Монте-Карло особенно эффективен для решения таких задач в которых результат нужен с небольшой точностью. Для решения задач методом Монте-Карло необходимо иметь источник случайных чисел. Обычно используют для этого аналитический способ получения псевдослучайных чисел, как наиболее простой и быстро реализуемый на компьютере. Единственный недостаток этого метода – ограниченность запаса псевдослучайных чисел. Исходной случайной величиной при использовании метода Монте-Карло является одномерная равномерная распределенная на промежутке [0,1] случайная величина α, т.е. случайная величина с плотностью распределения

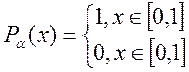
                    Имея в распоряжении реализацию случайной величины α можно получить реализацию случайной величины с заданным законом распределения. Пусть ξ  распределена по закону  F_ξ(x), тогда ξ= F^-1_ξ(α).

Например :

1) 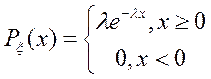, тогда .

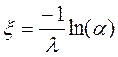2) Если ξ распределена по нормальному закону, имеющему среднее значение равное 0 и дисперсию равную 1 , то практически

.

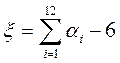Аналогично можно реализовать дискретные и многомерные случайные величины.

Рассмотрим вычисление интегралов методом Монте-Карло:

1)  Имеется алгоритм моделирования случайной величины, распределенной по закону F(x), тогда

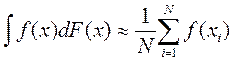
где  х_i - независимые реализации случайной величины с распределением F(x) . Погрешность этого метода убывает несколько медленнее , чем N^-½.

у A

          2)   В этом случае разыгрывается две случайные величины равномерно распределенные α  и   β .

0    a                    b    x   f(x)

Из N реализаций (α, β) в заштрихованной части оказалось m реализаций , тогда

            Рис.15.1

Интеграл оценивается с той же погрешностью, что и в случае (1).

3)    В случае двойного интеграла имеем :

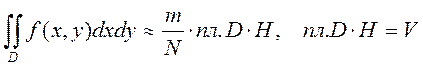
V- объем цилиндрического тела , содержащего искомый объем ;          N–количество реализаций (где α это равномерно распределенная случайная величина, принадлежащая интервалу [a,b] для переменной х; β для переменной γ; γ для переменной z ); m – количество реализаций ,попавших во внутреннюю часть искомого объема.

15.4  Пример выполнения работы

Вычислить 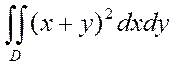 по области D с точностью  ε=0,02.

y                 D

Область D: 

4 2 0

1       2    2,5          4     х

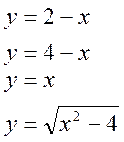
1≤х≤2,5 0≤у≤2 0≤z≤16

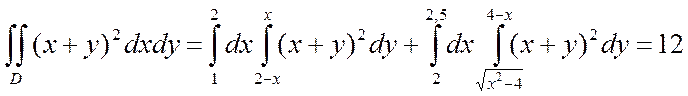
Вычисления в Mathcad :

Теперь воспользуемся встроенными функциями  для генерации случайных чисел:

Погрешность определения интеграла

          Δ=12-11.981=0.019   

Полученная погрешность не превышает заданной величины ε.

15.5   Порядок выполнения работы

1.  Ознакомится с методическими указаниями.

2.  Получить задание у преподавателя.

3.  Выполнить расчет  для N=1000 и N=10000.

4.  Рассчитать ошибку вычисления объема по методу Монте-Карло.

15.6 Содержание отчета

1.  Титульная страница с названием работы.

2.  Задание.

3.  Назначение работы и краткие теоретические сведения.

4.  Результаты ручных и автоматизированных  расчетов .

5.  Графические интерпретация .

6.  Выводы.

15.7   Контрольные вопросы

1.В чем состоит суть метода Монте-Карло ?

2.Достоинтсва и недостатки метода.

3.Приложение метода Монте-Карло.

4.Способы вычисления интегралов рассмотренным методом.

5. Роль равномерного  распределения  случайной величины .

6. Как осуществляется получение других распределений случайной величины, имея равномерное распределение.

15.8  Литература

1.Демидович Б.П., Марон И.Я., Основы вычислительной математики, М.:Наука,1996.

2.Ермаков С.М., Метод Монте-Карло и смежные вопросы,М.:Наука,1971.

3.Ермаков С.М., Михайлов Г.А., Статистическое моделирование, М:Наука,1982 .