Основным энергетическим процессом, происходящим в механизме, является преобразование работы движущих сил в работу сил полезного сопротивления, возникающих при выполнении рабочего процесса. Вместе с тем работа движущих сил переходит в механизме в кинетическую энергию его подвижных звеньев, потенциальную энергию действующих на звенья механизма потенциальных сил (силы тяжести, силы упругости в упругих элементах), а также в работу сил трения, возникающих в кинематических парах. При установившемся движении циклового механизма изменение кинетической и потенциальной энергий за цикл оказывается равным нулю, поскольку в начале и конце цикла координаты и скорости всех материальных точек одинаковы. Поэтому баланс работ за цикл может быть записан для механизма в следующей форме:
![]() , (6.1)
, (6.1)
где ![]() -
работа всех движущих сил,
-
работа всех движущих сил, ![]() - работа сил полезного
сопротивления,
- работа сил полезного
сопротивления, ![]() - работа сил трения,
характеризующая потери энергии в механизме. Работа си трения, преобразующаяся в
тепловую энергию, приводит к нагреву контактирующих элементов кинематических
пар, что вызывает увеличение интенсивности износа и снижение долговечности
механизма. Расходы энергии на трение ухудшают экономические показатели работы
машины.
- работа сил трения,
характеризующая потери энергии в механизме. Работа си трения, преобразующаяся в
тепловую энергию, приводит к нагреву контактирующих элементов кинематических
пар, что вызывает увеличение интенсивности износа и снижение долговечности
механизма. Расходы энергии на трение ухудшают экономические показатели работы
машины.
В связи с этим потери на трение, возникающие в механизме при выполнении заданного рабочего процесса, должны рассматриваться как одна из важных динамических характеристик, определяющих качество механической системы машины.
 После проведения
кинематического и силового анализа и определения сил трения в кинематических
парах вычисление потерь энергии в механизме не вызывает затруднений. Рассмотрим
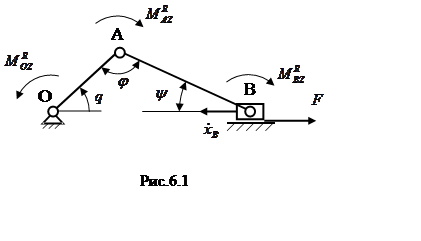
в качестве примера кривошипно-ползунный механизм, показанный на рис.6.1.
Предположим, что в некотором положении механизма, определяемой обобщенной
координатой
После проведения
кинематического и силового анализа и определения сил трения в кинематических
парах вычисление потерь энергии в механизме не вызывает затруднений. Рассмотрим
в качестве примера кривошипно-ползунный механизм, показанный на рис.6.1.
Предположим, что в некотором положении механизма, определяемой обобщенной
координатой ![]() , найдены величины силы трения
, найдены величины силы трения ![]() в поступательной паре и моменты сил
трения во вращательных парах
в поступательной паре и моменты сил
трения во вращательных парах ![]() ,
, ![]() ,
, ![]() . Тогда,
зная скорость движения ползуна
. Тогда,
зная скорость движения ползуна ![]() и относительные угловые
скорости
и относительные угловые
скорости ![]() ,
, ![]() ,
, ![]() во вращательных парах
во вращательных парах ![]() ,
, ![]() ,
, ![]() , можно определить мощность сил трения
, можно определить мощность сил трения
![]() . (6.2)
. (6.2)
Работа сил трения за цикл
при равномерном вращении входного звена с угловой скоростью ![]() определяется интегрированием этого
выражения:
определяется интегрированием этого
выражения:
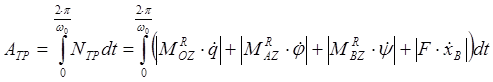 .
.
Учитывая, что
![]() ;
; 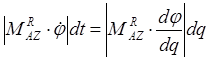 ;
;
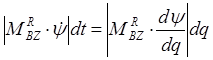 ;
; 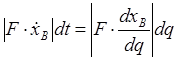 ;
;
получаем
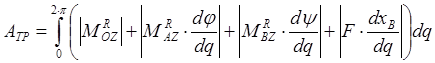 . (6.3)
. (6.3)
Для приближенного вычисления
этого интеграла определяются значения сил и моментов сил трения, а также
геометрические передаточные функции механизма ![]() ,
, ![]() ,
, ![]() в
в ![]() дискретных положениях (
дискретных положениях (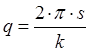 ,
, ![]() ).
Далее вычисляется приближенное значение
).
Далее вычисляется приближенное значение ![]() по
формуле
по
формуле
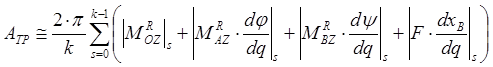 . (6.4)
. (6.4)
Качество механизма может характеризоваться и таким параметром, как коэффициент полезного действия (КПД). Коэффициентом полезного действия циклового механизма при установившемся движении называется отношение работы сил полезного сопротивления за цикл к работе движущих сил:
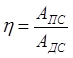 . (6.5)
. (6.5)
Для передаточных механизмов с линейной функцией положения КПД может быть определен как отношение мощности полезных сил сопротивления к мощности движущих сил. Величина
![]() , (6.6)
, (6.6)
равная в силу выражения (6.1), отношению потерь на трение к работе движущих сил, называется коэффициентом потерь.
Напомним, что реакции в
кинематических парах, а следовательно, и возникающие в них силы трения, зависят
как от активных сил полезного сопротивления, так и от сил инерции. Силы инерции
в свою очередь определяются законами движения звеньев. Поэтому КПД и
коэффициент потерь зависят не только от качества механизма, свойств его
кинематических пар, коэффициентов трения в них, но и от режима работы, законов
программного движения, рабочей нагрузки. Так, при полном отсутствии полезной нагрузки
(![]() ), силы инерции звеньев механизма будут
вызывать реакции в кинематических парах, а следовательно, и силы трения. В этом
режиме всегда
), силы инерции звеньев механизма будут
вызывать реакции в кинематических парах, а следовательно, и силы трения. В этом
режиме всегда ![]() ,
, ![]() . С увеличением
рабочей нагрузки при фиксированном законе движения входного звена КПД механизма
будет возрастать, поскольку потери на трение будут увеличиваться медленнее, чем
работа сил полезного сопротивления.
. С увеличением
рабочей нагрузки при фиксированном законе движения входного звена КПД механизма
будет возрастать, поскольку потери на трение будут увеличиваться медленнее, чем
работа сил полезного сопротивления.
Чтобы исключить влияние инерционных сил на КПД, можно пользоваться условной расчетной моделью механизма, учитывающей только действие движущих сил и сил полезного сопротивления. В этой модели принимается, что массы всех звеньев равны нулю.
Силы трения, рассчитанные по такой модели, будут в каждом положении механизма пропорциональными полезной нагрузке, и КПД будет характеризовать только свойства кинематических пар.
Для увеличения КПД и уменьшения потерь на трение при конструировании механизмов используются различные методы. Наибольший эффект дает уменьшение коэффициентов трения в кинематических парах.
 При движении механизмов
возникают переменные силы, действующие на корпус машины. Такие силы возникают
прежде всего в кинематических парах, соединяющих подвижные звенья механизма с
корпусом. Так, например, механизм, показанный на рис.6.2, воздействует на
корпус силами
При движении механизмов
возникают переменные силы, действующие на корпус машины. Такие силы возникают
прежде всего в кинематических парах, соединяющих подвижные звенья механизма с
корпусом. Так, например, механизм, показанный на рис.6.2, воздействует на
корпус силами ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
возникающими в шарнирах
,
возникающими в шарнирах ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Равные и противоположно направленные
силы
. Равные и противоположно направленные
силы ![]() ,
, ![]() ,
, ![]() ,
, ![]() приложены
к звеньям механизма со стороны корпуса; в дальнейшем мы их будем называть
внешними реакциями и обозначать через
приложены
к звеньям механизма со стороны корпуса; в дальнейшем мы их будем называть
внешними реакциями и обозначать через ![]() , где
, где ![]() - номер звена, к которому приложена
соответствующая сила.
- номер звена, к которому приложена
соответствующая сила.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.