Динамические характеристики механизмов с жесткими звеньями, страница 3

Если все активные силы, приложенные к звеньям механизма, являются внутренними для машины в целом, уравновешенность машины будет обеспечиваться при выполнении условий

;  ,                                                     (6.12)

то есть при уравновешенности сил инерции.

За меру неуравновешенности механизма, его внешней виброактивности, естественно принять величины главного вектора  и главного момента  его внешних реакций. Следует однако иметь в виду, что при   величина  зависит от выбора центра приведения . Поэтому  может рассматриваться как мера неуравновешенности только при фиксированном положении точки . Вообще же не зависящим от центра приведения является, как известно, скалярное произведение .

В современных быстроходных машинах уравновешивание механизма и машины в целом не решает полностью задачу устранения внешней виброактивности. Уравновешенные силы, приложенные к корпусу в различных точках, могут вызывать его деформации и приводить к интенсивным колебаниям. Не следует также думать, что внутренние активные силы, не входящие в условие (6.12), вообще не влияют на уровень внешней виброактивности. 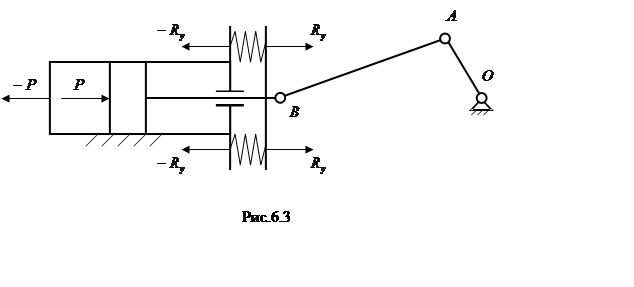Следует помнить, что эти силы влияют на закон движения механизма, а следовательно, и на величины сил инерции. Так, например, внутренние силы  и , показанные на рис.6.3, могут вызывать неравномерность вращения кривошипа , что приведет к изменению воздействия машины на основание.

3.  Методы уменьшения внешней виброактивности плоских механизмов.

При анализе внешней виброактивности плоского механизма часто ограничиваются определением составляющих главного вектора и главного момента внешних реакций, лежащих в плоскости движения. Если располагать оси  и  в этой плоскости, тот речь пойдет о компонентах , , . Для каждого положения механизма может быть найдена прямая , параллельная вектору , являющаяся линией действия равнодействующей всех внешних реакций  (рис.6.4). Ее положение определяется из условия

,                                        (6.13)

где  - точка, лежащая на прямой  (например, точка пересечения оси  с этой прямой),  - расстояние от точки до прямой .  В процессе движения механизма величина и направление вектора изменяются, меняется также положение прямой .

Установка противовесов на звеньях. Пусть все активные силы (кроме сил тяжести, влияние которых здесь учитываться не будет) являются внутренними для машины в целом. Тогда

,                                                     (6.14)

где  - вектор абсолютного ускорения центра масс механизма. Поскольку при плоском движении вектор  лежит в плоскости движения, вектор   также лежит в этой плоскости. Из (6.14) вытекает, что первое из условий уравновешенности (6.11)  выполняется, если , то есть если . Но для стационарной машины скорость  , будучи постоянной, не может отличаться от нуля. Таким образом, для выполнения условия  должно быть  , то есть центр масс всего механизма должен оставаться неподвижным в процессе движения. В принципе это условие можно выполнить установкой на звеньях механизма дополнительных масс-противовесов. На рис.6.5 показан способ уравновешивания кривошипно-ползунного механизма с помощью двух противовесов, установленных на шатуне и кривошипе. Пусть , ,  - центры масс кривошипа, шатуна и ползуна; , ,  - массы этих звеньев; ,  - центры масс противовесов; . Выбрав массу первого противовеса из условия

,

мы перенесем центр масс системы шатун- ползун в точку . Далее речь должна идти о приведении центра масс системы в точку . Для этого должно выполняться условие

.