Динамические характеристики механизмов с жесткими звеньями, страница 4

Недостатком такого способа уравновешивания является очень большая суммарная масса противовесов. Действительно, пусть

, .                 (6.15)

Из первого и второго условия получим  массы противовесов

,  .

Таким образом, суммарная масса противовесов более чем в три раза превосходит массу всех подвижных звеньев механизма. В результате резко возрастает его внутренняя виброактивность и ухудшаются динамические свойства.

Конструктивное уравновешивание. Привести центр масс механизма к неподвижной точке можно, создавая параллельные механизмы (рис.6.6). По сравнению с предыдущим методом мы увеличиваем массу механизма всего в два раза.

Отметим, что при установке противовесов на звеньях и в случае конструктивного уравновешивания не будет выполняться условие ; момент  будет создаваться внешними реакциями , ,  (рис.6.5, 6.6).

Установка вращающихся противовесов. Пусть входное звено исполнительного механизма (кривошипа) вращается с угловой скоростью (рис.6.5). Полагая, что активные силы для машины являются внутренними, имеем

;

.

Здесь ,  - координаты центра масс механизма, являющиеся периодическими функциями угла поворота кривошипа ; ,  - вторые производные по , также являющиеся периодическими функциями;  - масса подвижных звеньев механизма. Разложим функции  и  в ряд Фурье и сохраним в этом ряду только первую гармонику:

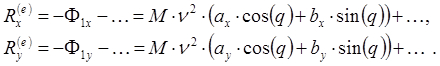                    (6.16)

Часто первая гармоника сил инерции  является наибольшей. Покажем, что всегда можно установить два вращающихся противовеса  и  (рис.6.7) так, чтобы выполнялось условие

.                                                     (6.17)

При этом противовес  закреплен на кривошипе, а  установлен на дополнительном валу, связанном с кривошипом зубчатой передачей внешнего зацепления с . Запишем выражение (6.17) в проекции на оси:

,

.

Приравняем коэффициенты при  и :

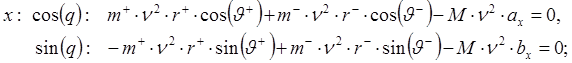
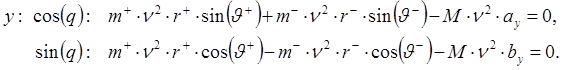
После несложных преобразований получаем:

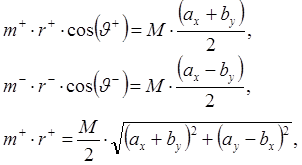
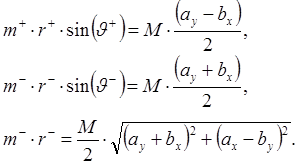            (6.18)

Определим массы противовесов и углы их установки для механизма рис.6.7, если длины звеньев и массы определяются выражением (6.15). Координаты точек  ,  и их вторые производные по (аналоги ускорения):

, , , ,

, ,

.

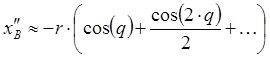Запишем выражение для первой гармоники главного вектора сил инерции (в  оставляем только первое слагаемое):

,

.

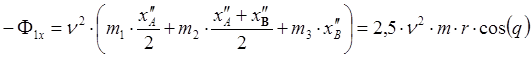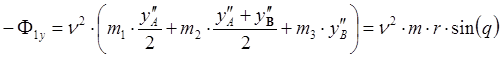Учитывая, что масса механизма , из (6.16) получаем коэффициенты при  и :

, , , .

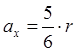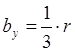Принимаем радиусы установки противовесов . Из (6.18) определяем углы установки противовесов и их массы:

, , .

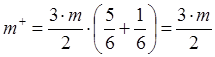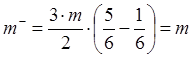Как видим, противовесы в этом случае оказываются менее громоздкими (их суммарная масса для рассмотренного примера равна половине массы подвижных звеньев механизма), однако при этом появляется дополнительная зубчатая передача.

Чаще всего ограничиваются установкой одного противовеса, уменьшающего первую гармонику неуравновешенной силы, но не обеспечивающего полное ее устранение. Можно, например, выбрать величину массы противовеса, радиуса и начального угла его установки на кривошипе таким образом, чтобы минимизировать наибольшее значение модуля .

 

Повторить по лекции 20:

Коэффициент полезного действия ;	Методы уменьшения внешней виброактивности плоских механизмов:
Коэффициент потерь ;	- установка противовесов на звеньях,
Внешняя виброактивность механизмов и машин;	- конструктивное уравновешивание,
Мера внешней виброактивности;	- установка вращающихся противовесов;
Влияние внутренних и внешних активных сил на внешнюю виброактивность;	Сравнение различных методов уравновешивания механизмов.