{длинна меньший обломка не превосходит 1/3 длины стержня}
Пространство элементарных исходов в этом случае будет состоять из трёх равновероятных исходов:
![]() , где
, где
w1 = { разлом произошел на отрезке от 0 до 1/3 длины стержня },
w2 = { разлом произошел на отрезке от 1/3 до 2/3 длины стержня },
w3 = { разлом произошел на отрезке от 2/3 до длины стержня },
Интересующему нас событию. А благоприятны два элементарных
исхода, т. е. ![]() .
.
Применим классический метод
вычисления вероятностей. Исходя из него вероятность возникновения события А
равна 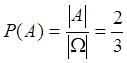
Ответ: 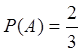
Задача №4
На участке АВ движения поезда имеется 12 светофоров. Вероятность остановки перед каждым из них равна 0.1. Вероятность того, что от пункта В до конечного пункта С поезд пройдет без остановки, равна 0.7. Определить вероятность того, что участок АС поезд пройдет без остановки.
Решение.
Рассмотрим вероятность того, что
поезд не остановится перед любым светофором, она равна Рi = 1-0.1 = 0.9. Поскольку чтобы
пройти участок АВ без остановки поезд не должен остановится не перед одним
светофором, то вероятность того, что поезд не остановится на участке АВ, равна ![]() .
.
Исходя из сказанного, делаем вывод,
что вероятность того, что поезд не остановится на участке АС, равна ![]() , где РВС есть вероятность прохода поездом участка ВС без остановки.
, где РВС есть вероятность прохода поездом участка ВС без остановки.
Рассчитаем перечисленные вероятности:
РАВ = 0.9*0.9*..*0.9 = 0.912 = 0.282429536
![]() = 0.282429536*0.7 =
0.1977
= 0.282429536*0.7 =
0.1977
Ответ: РАС = 0.1977
Задача №5
Игра между А и В ведётся на следующих условиях: в результате первого хода, который всегда делает А, он может выиграть с вероятностью 0.3. Если первым ходом А не выигрывает, то ход делает В и может выиграть с вероятностью 0.5. Если в этом ходу В не выиграет, то А делает второй ход, который может привести к выигрышу с вероятностью 0.4. Определить вероятность выигрыша В.
Решение.
Поскольку вероятность выигрыша А на первом ходу равна 0.3, то вероятность того, что А не выиграет равна P!A = 1-0.3 = 0.7. Отсюда можем сделать вывод, что В выиграет с вероятностью равной произведению вероятности того что не выиграет А и заданной в условии вероятности выигрыша В при условии что А не выиграл на первом ходу.
![]() Значит:
Значит:
PB = P(B|A) Ç P!A = 0.5*0.7 = 0.35
Ответ: РВ = 0.35
Задача №7
В тире имеется девять ружей, из которых пристрелянными являются только два. Вероятность попадания в цель из пристрелянного ружья равна 0.8, а из не пристрелянного – 0.1. Выстрелом из одного наугад взятого ружья мишень поражена. Определить вероятность того, что взято пристрелянное ружьё.
Решение.
В результате проведения вероятностного эксперимента было выяснено что событие А = {выстрелом из выбранного наугад ружья цель поражена} выполнилось. В связи с этим можно выдвинуть две гипотезы:
H1 = {было выбрано пристрелянное ружьё},
H2 = {было выбрано не пристрелянное ружьё}.
Исходя из сделанных предположений, по формуле Байерса, можем найти вероятность того, что было выбрано пристрелянное ружьё. Для того чтобы применить формулу Байерся произведём следующие расчеты:
Исходя из условия Р(H1) = 2/9 = 0.(2), Р(H2) = 7/9 = 0.(7), Р(А| H1) = 0.8,
Р(А| H1) = 0.1.
Применим формулу Байерса:
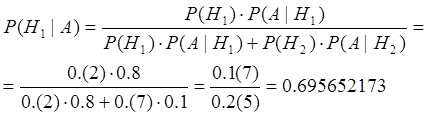
Ответ: P(H1|A) = 0.695652173
Задача №8
Вероятность попадания стрелком в десятку равно 0.7, а в девятку – 0.3. Определить вероятность того, что данный стрелок при трех выстрелах наберёт не менее 29 очков.
Решение.
Рассмотрим данный эксперимент. Стрелок наберёт 29 или 30 очков только в следующих случаях:
1) Если он поразит десятку со всех трёх выстрелов.
2) Если с двух выстрелов он поразит десятку, а с одного – девятку, причем делать он это может в любом порядке.
Отсюда вытекает, что вариантов набора может быть всего четыре. Поэтому вероятность мы можем рассчитать по формуле:
![]() ,
,
где Р10 = 0.7 – вероятность поразить десятку, Р9 = 0.3 – вероятность поразить девятку. Подставив в данную формулу заданные значения вероятностей, получим Р – искомую вероятность.
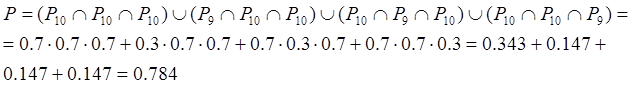
Ответ: P = 0.784
Задача №9
Депо производит ремонт вагонов. Вероятность того, что ремонт будет произведён со сдачей с первого предъявления, равна 0.8. Найти вероятность того, что из ста вагонов, отремонтированных в депо:
а) ровно 50 вагонов будут сданы с первого предъявления;
б) от 40 до 80 вагонов будут сданы с первого предъявления;
Решение.
По условию задачи проводятся n = 100 независимых испытаний, проверяется качество ремонта, и вероятность появления «успеха» ( ремонт произведён со сдачей с первого предъявления) в каждом испытании Р = 0.8; соответственно вероятность «неудачи» Q = 1-P = 1-0.8 = 0.2. Для нахождения искомой вероятности события
а) A = { ровно 50 вагонов будут сданы с первого предъявления
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.