МИНИСТЕРСТВО ОБРАЗОВАНИЯ
РЕСПУБЛИКИ БЕЛАРУСЬ
Кафедра “Прикладная математика ”
Расчётно-графическая работа №1
Выполнил: Проверил:
студент гр. УД-21 преподаватель
Савкин С.А. Евдокимович В.Е.
Гомель 2004
Задача №1
Вероятностный эксперимент состоит в том, что внутри квадрата выбирается наугад точка. Рассмотрим три события:
Решение
А= { выбранная точка лежит внутри круга А },
B= { выбранная точка лежит внутри круга В },
C= { выбранная точка лежит внутри круга С },
__ _ _ ____ ______
Заштриховать области соответствующие событиям: АВ· С, А+В-С, А· (В-С), А· В-С.
1.
__ __ _
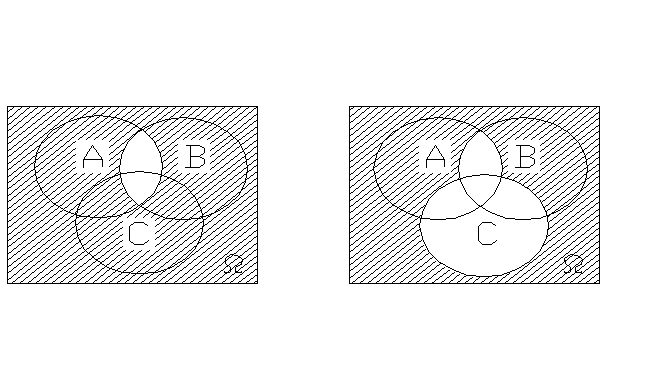
АВ АВ· С
2.
_ _
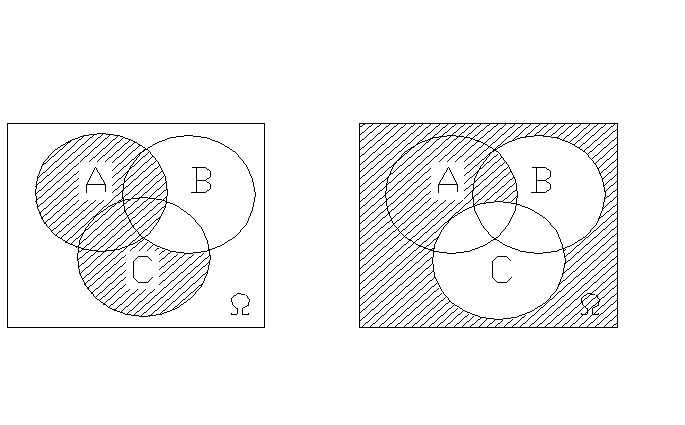
А+В А+В-С
3.
_____ ____
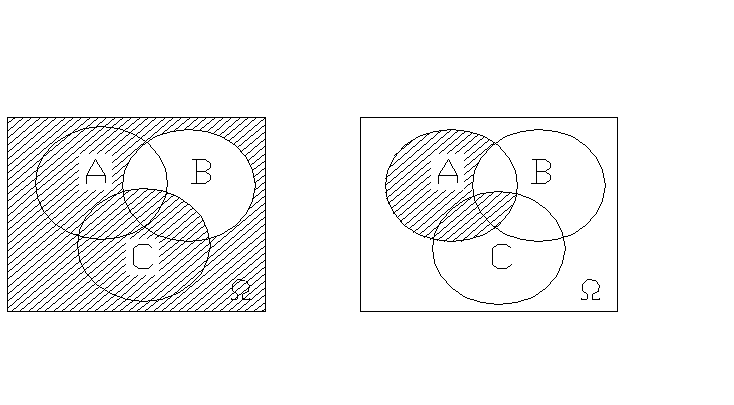
(В-С) А· (В-С)
4.
______
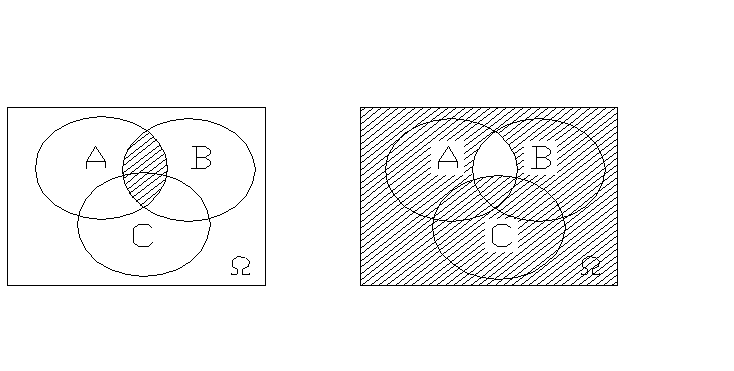
А·В А·В-С.
Задача№2
Из урны, содержащей 20 пронумерованных шаров, наугад вынимается 20 шаров. После каждого вынимания шар возвращается в урну и перемешивается с другими, а номер его записывается. Найти вероятность того, что будет записана последовательность номеров 1, 2, … 20.
Решение
Е: Извлечение шаров из урны в определенной последовательности
А: {Шары извлекаются в последовательности от 1 до 20 }
Р(А)-?
Пространство элементарных событий Ω конечно
___
Ω = { ω | i=1,n}
где элементарное событие
ω = {выбрано 20 шаров из 20}
Число n элементарных событий пространства Ω – это число различных комбинаций шаров
~
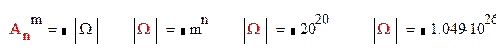
Событию А соответствует
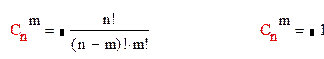
Найдем вероятность события А
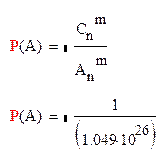
Ответ: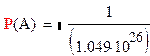 
-
это вероятность записи номеров 1, 2, … 20.
Задача№3
Внутрь круга радиуса R наугад брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг правильного треугольника.
Решение
Е: бросание точки в круг
А:{ точка оказывается внутри вписанного в круг правильного треугольника}
Р(А)-?
Данную задачу возможно решить геометрическим методом. Естественно, что пространством Ω элементарных событий этого эксперимента является площадь круга S1, тогда событию А соответствует площадь треугольника S2.Следовательно, вероятность события А можно найти из следующей формулы
Р(А)=S2/S1
Запишем формулы для нахождения S2 и S1.
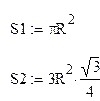
Находим вероятность попадания точки в треугольник
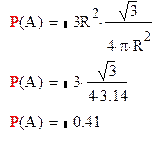
Ответ: Р(А)=0,41.
Задача№4
Прибор состоит из двух
элементов, работающих независимо. Вероятность выхода из строя первого элемента
при включении прибора – 0,05, второго – 0,08. Найти вероятность того, что при
включении прибора выйдет из строя только первый элемент.
Решение
Е: включение прибора
А={выход из строя первого элемента}=0,05
В={выход из строя второго элемента}=0,08
С={выход из строя только первого элемента}
Р (С)-?
Очевидно, что условие задачи выполнится если произойдет событие А , и одновременно не произойдет событие В , т. е.
_ _
Р(С)=Р(АВ)=Р(А) 
Р(В)=0,05· (1-0,08)=0,046
Ответ: Р(С)=0,046.
Задача№5
Стрелок попадает в мишень, разделенную на 3 непересекающиеся части. Вероятность попадания в первую часть 0,45, во вторую 0,35. Найдите вероятность того, что при одном выстреле стрелок попадает либо в первую, либо во вторую часть.
Решение
Е: попадание в мишень
А={попадание в первую часть}=0,45
В={попадание во вторую часть}=0,35
С={попадание в третью часть}=1-(0,45+0,35)=0,2
Р(А U В)-?
Событие А не зависимо от события В, т. к. вероятность А не изменится при наступлении В, тогда
Р(А U В)=Р(А)+Р(В)=0,45+0,35=0,8
Ответ: Р(А U В)=0,8.
Задача№6
Происходит бой между двумя самолетами: истребителем и бомбардировщиком. Стрельбу начинает истребитель: он дает по бомбардировщику один выстрел и сбивает его с вероятностью 0,75. Если бомбардировщик этим выстрелом не сбит, он стреляет по истребителю и сбивает его с вероятностью 0,7. Если истребитель не сбит, он еще раз стреляет по бомбардировщику и сбивает его с вероятностью 0,6. Найти вероятность того, что сбит бомбардировщик. Р=0,795.
Решение
Е: дуэль двух самолетов
А={поражение истребителя}
В={поражение бомбардировщика}
Р(А)-?
Р(В)-?
Для выполнения А необходимо совмещение (произведение) двух событий
Р(А)=0.25·0.7=0.175
Для выполнения В необходимо выполнение двух несовместных событий
В1={ поражение бомбардировщика первым выстрелом истребителя}
В2={ поражение бомбардировщика вторым выстрелом истребителя}
Р(В)= Р(В1)+ Р(В2)
Р(В1)=0,75
Р(В2) состоит из трех совместных событий:
1)первый выстрел истребителя не поражает бомбардировщик(0.25)
2) ответный выстрел бомбардировщика не поражает истребитель(0.3)
3) второй выстрел истребителя поражает бомбардировщик(0,6)
Р(В2)=0,25·0,3·0,6=0,045
Р(В)= 0,75+0,045=0,795
Ответ: Р(В)= 0,795
Задача№7
Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит 60% деталей отличного качества, а второй – 84%. Наугад взятая деталь оказалась отличного качества. Найти вероятность, что эта деталь произведена первым автоматом.
Решение
Е: выбор детали из общего количества
А={выбранная деталь отличного качества }
В={выбранная деталь отличного качества и произведена первым автоматом}
Р(В)-?
Среди общего количества деталей 2/3 – это детали произведенные первым автоматом, а 1/3 – вторым.
Рассмотрим две гипотезы:
Н1={деталь произведена первым автоматом}
Н2={деталь произведена вторым автоматом}
Следовательно, Р(Н1)=2/3, Р(Н2)=1/3.
Р(А| Н1)=0.6, Р(А| Н2)=0.84
Искомая вероятность
Р(Н1) ·Р(А| Н1) 2/3·0,6
Р(Н1|А)=Р(В)= ---------------------------------------------- = ------------------------ =0,58
Р(Н1) · Р(А| Н1)+ Р(Н2) · Р(А| Н2) 2/3·0,6+1/3·0.84
Ответ: Р(В)=0,58.
Задача№8
При осмотре в парке отправления составов в каждом из них с вероятностью 0,3 обнаруживаются вагоны, требующие ремонта. Определить наивероятнейшее число составов, в которых есть такие вагоны, если в сутки со станции отправляется 100 поездов.
Решение
Е: проверка вагонов
А={обнаружение вагона, требующего ремонта}
Р(А)=0,3
n=100
k-наивероятнейшее число составов в которых есть вагоны, требующие
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
