Методика эксперимента «Инструментализация способа сокращенного умножения», страница 3

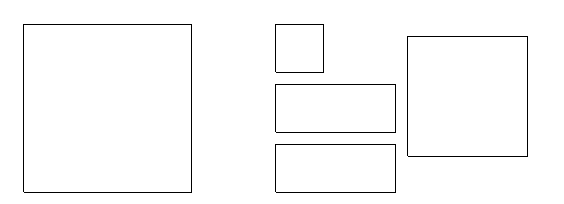
рис. 1

Полученное равенство фиксируется на доске схематически. Далее полученное равенство геометрических фигур моделируется на другом математическом языке – на алгебраическом языке. Отмечается, что установленное равенство является равенством площадей квадрата и набора фигур. Моделируется на алгебраическом языке площадь каждой фигуры: . И равенство фигур записывается теперь уже на алгебраическом языке: .

2.  Доказательство формулы;

На этом этапе урока ведущий отмечает необходимость доказательства следующим образом: он предлагает испытуемым задание: «Проверить полученную формулу для чисел a=123567 и b=876433». Проверять формулу, подставляя эти числа, оказывается очень долго и неудобно. Испытуемые приходят к выводу, что для того, чтобы убедиться в том, что равенство  выполняется для всех чисел, необходимо это равенство доказать. При доказательстве испытуемые используют распределительный закон и знание о натуральной степени.

3.  Проверка уяснения. Ведущий контролирует правильность выполнения заданий. Испытуемые выполняют задания на применение формулы.

Таким образом, на первом этапе эксперимента в форме коллективно-распределенной деятельности в группе 1 и группе 2 было сформировано понятие сокращенного умножения соответственно содержательно-эмпирическим и содержательно-теоретическим обобщениями.

Диагностика типа и качества обобщения проводилась нами и являлась общей для первой и для второй группы испытуемых. Для диагностики использовалась упрощенная методика В.А. Крутецкого. Форма проведения диагностики – индивидуальная беседа с испытуемым.

Материалом методики является система однотипных заданий, так называемая «лестница задач». Все задачи этой системы являются задачами на применение формулы сокращенного умножения  - и расположены в порядке усложнения:

1.

2.

3.  

4.

5.

6.

7.

8.

Сначала испытуемому предлагается решить самую сложную задачу №8 (конечное звено): . Если испытуемый затрудняется, то ему предлагается решить задачу №2. После решения задачи №2, испытуемому опять предлагается решить задачу №8. Если испытуемый опять затрудняется её решить, ему предлагается задача №3. Так продолжается до тех пор, пока испытуемый не решит конечную задачу №8.

Заметим, что упрощение нами методики В.А. Крутецкого состоит в том, что испытуемым не предлагаются задачи, внешне напоминающие задачи на применение формулы, но по существу совершенно отличные, например . Таким образом, испытуемый должен только обобщить задачи на применение формулы сокращенного умножения. То есть от испытуемого не требуется отдифференцировать от задач на применение формулы задачи, не относящиеся к использованию этой формулы. 

Если испытуемый «сходу» решает задачу №8, это говорит о том, что способ действия у него сформирован теоретически. Если же испытуемому требуется некоторое число промежуточных шагов для решения задачи №8, это свидетельствует о том, что общий способ сформирован эмпирически. С помощью представленной методики можно количественно оценить качество эмпирического обобщения. Качество эмпирического обобщения характеризуется количеством частных случаев, на основе анализа которых обобщается способ действия. Показателем качества эмпирического обобщения в этом случае является количество частных случаев необходимых для обобщения способа.