Методика эксперимента «Инструментализация способа сокращенного умножения», страница 2

Целью третьего этапа является диагностика степени инструментализации математического действия у каждого отдельного испытуемого. Методика третьего этапа разработана на основании выдвинутых нами характеристик решения задач-ситуаций, требующих функционализации способа:

ü Идентификация задачи, как востребующей применение способа;

ü Трансформация способа действия для решения задачи.

Степень инструментализации действия определяется параметрами решения испытуемым задач, требующих использование способа: идентифицирует ли испытуемый задачу как востребующую применение общего способа, трансформирует ли способ, если это необходимо для решения задачи.

§3.2. Характеристика этапов эксперимента

Итак, эксперимент состоял из трех этапов:

ü этап, формирующий тип обобщения;

ü этап, диагносцирующий тип и качество обобщения;

ü этап, диагносцирующий степень инструментализации действия.

Для осуществления первого этапа нами были разработаны проекты формирования понятия сокращенного умножения, которые прошли экспертную оценку и в результате были исправлены и дополнены. Формирование понятий в двух группах испытуемых проводила Юдина Юлия Геннадьевна, опытный преподаватель гимназии «Универс».

В первой группе понятие сокращенного умножения формируется содержательно-эмпирическим обобщением. Для этого организуется ситуация сравнения и преобразования эмпирического материала  с целью выделения общего способа действия. Нами выявлено, что результаты эмпирического обобщения нуждаются в доказательстве (см. гл. 2). Следовательно, следующим этапом после вывода формулы сокращенного умножения должен быть этап доказательства этой формулы.

Этапы формирования понятия содержательно-эмпирическим обобщением:

1.  Получение материала для сравнения. Испытуемые выполняют задание: «Дописать правые части равенств 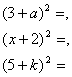», используя знание о степени и распределительный закон. Ведущий проверяет правильность выполнения задания; задает наводящие вопросы: «Как найти чему равно?», «Какой закон поможет?», «Что такое степень?»;

2.  Вывод общего правила. Испытуемые сравнивают полученные равенства, находят общие признаки. Ведущий задаёт ученикам указывающие и наводящие вопросы;

В результате выполнения задания были получены следующие равенства: 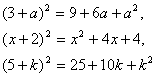. И основная трудность при выводе формулы сокращенного умножения заключалась в том, что испытуемые при сравнении этих трех равенств не могли «увидеть» удвоенное произведение. Выделение удвоенного произведения как элемента формулы сокращенного умножения является необходимым для вывода общего способа  преобразованием эмпирического материала. Это позволяет говорить о формуле сокращенного умножения как о результате содержательно-эмпирического обобщения. 

3.  Фиксация общего правила, его доказательство. Ведущий фиксирует общее правило – формулу на доске, отмечает необходимость доказательства формулы. Испытуемые доказывают общую формулу, используя при этом распределительный закон и знание о степени;

4.  Решение аналогичных примеров – отработка. Испытуемые решают у доски аналогичные примеры. Ведущий контролирует правильность выполнения аналогичных заданий.

Во второй группе испытуемых понятие сокращенного умножения формируется содержательно-теоретическим обобщением (обобщением через построение модели в иной математической теории). Для этого организуется предметное действие – сравнение геометрических фигур, результаты которого записываются на алгебраическом языке, то есть моделируются средствами другой математической теории.

Этапы формирования понятия содержательно-теоретическим обобщением:

1.  Формула как модель равенства объектов;

Испытуемые выполняют предметное действие - сравнение фигурок из картона: квадрата со стороной  и набора: квадрат со стороной , квадрат со стороной  и два прямоугольника  (см. рис. 1).