Так как R0 > N и R0 больше действительного нажатия токоприемника P, то разгрузки подрессорных струн не произойдет. Подъем контактного провода ∆h0 определим по выражению [1, стр. 85, ф.148], м.
|
|
(55) |
Значение коэффициента γ1 определим по выражению [1, стр. 85, ф.150]
|
|
(56) |
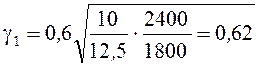
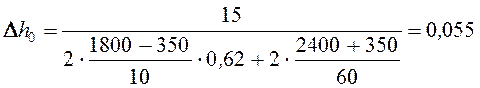 м
м
Для точки 0' ∆h0' = 0,055 м.
3. Определение эластичности э0 и жесткости ж0 в точке 0 и 0'.
|
э0 = ∆h0 / Р = 55 / 15 = 3,67 мм/даН ж0 = Р / ∆h0 = 15 / 0,055 = 273даН/м |
э0' = ∆h0' / Р = 55 / 15 = 3,67 мм/даН ж0' = Р / ∆h0' = 15 / 0,055 = 273даН/м |
4. Определение подъема контактного провода в точке 1.
Сравним расчетное нажатие токоприемник N1 с силой R1, при которой начинается разгрузка околоопорной струны, и расчетное нажатие токоприемник N'1 с силой R'1, при которой начинается разгрузка соседних с этой точкой струн.
Значение N1, даН, определим по выражению [1, стр. 82, ф.143]
|
|
(57) |
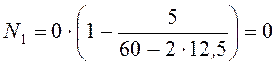 даН
даН
Значение N'1, даН, определим по выражению [1, стр. 82, ф.144]
|
|
(58) |
 даН
даН
Значение R1, даН, определим по выражению [1, стр. 82, ф.139]
|
R1 = nкgк · 0,5(c – a1 + c1) + G'c + N1 |
(59) |
R1 = 1 · 1,05 · 0,5 · (12,5 – 2,5 + 5) + 0,3 + 0 = 16,05 даН
Значение R'1, даН, определим по выражению [1, стр. 82, ф.140]
|
R'1 = nкgк · (c + 1,5c1) + 3G'c + N'1 |
(60) |
R'1 = 2 · 1,05 · (12,5 + 1,5 · 5) + 3 · 0,3 + 0 = 42,9 даН
Так R1 > P, то околоопорные струны не будут разгружены. Поэтому подъем контактного провода ∆h1, м, определим по выражению [1, стр. 85, ф.152]
|
|
(61) |
В последнем выражении
γ3 = а(1 – 0,05а) / с = 10 · (1 – 0,05 · 10) / 12,5 = 0,4
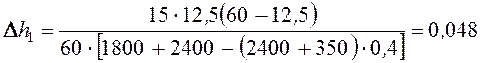 м
м
5. Определение эластичности э1, мм/даН, и жесткости ж1, даН/м, в точке 1.
э1 = 48 / 15 = 3,2 мм/даН
ж1 = 15 / 0,048 = 313 даН/м
6. Определение подъема контактного провода в точках 2, 23, 3, 34, 4 и 45.
Определение значения силы Rc, даН, при которой начинается разгрузка струн в этих точках [1, стр. 82, ф.141].
|
Rc = (nкgкcc + G'c – Nc)(T + К) / Т |
(62) |
Значение Nc, даН, в этом выражении найдем по формуле [1, стр. 82, ф.145]
|
Nc = 8fКcc / (l – 2c)2 |
(63) |
Nc = 8 · 0 · 2400 · 5 / (60 – 2 · 12,5)2 = 0 даН
Rc = (2 · 1,05 · 5 + 0,3– 0)(1800 + 2400) / 1800 = 25,2 даН
Так как Rc > P, то струны в точках 2, 3 и 4 не будут разгружаться. Ввиду того, что 2Rc > 15 даН, то воздействие токоприемника в точке 45 не приведет к разгрузке струн в точках 4 и 5. Подъем контактного провода, м, в точках 2, 3, 4 можно определить по выражению [1, стр. 85, ф.158]
|
|
(64) |
|
где х – расстояние от точки подвешивания несущего троса до соответствующей струны ( расчетной точки ), м. |
|
Для струны в точке 2
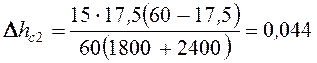 м
м
Соответственно для струн в точках 3 и 4
∆hс3 = 0,05 м
∆hс4 = 0,053 м
Подъемы контактного провода в токах 23, 35, 45 определим по выражению [1, стр. 85, ф.161]
|
|
(65) |
Для точки 23
 м
м
Соответственно подъемы контактного провода в точках 34 и 45
∆h'с34 = 0,055 м
∆h'с45 = 0,057 м
7. Определение эластичностей и жесткостей в пролете в точках 2, 23, 3, 34, 4 и 45.
|
э2 = 44 / 15 = 2,93 мм/даН ж2 = 15 / 0,044 = 341 даН/м |
э3 = 50 / 15 = 3,33 мм/даН ж3 = 15 / 0,05 = 300 даН/м |
|
э4 = 53 / 15 = 3,53 мм/даН ж4 = 15 / 0,053 = 283 даН/м |
э23 = 51 / 15 = 3,4 мм/даН ж23 = 15 / 0,051 = 294 даН/м |
|
э34 = 55 / 15 = 3,67 мм/даН ж34 = 15 / 0,055 = 273 даН/м |
э45 = 57 / 15 = 3,8 мм/даН ж45 = 15 / 0,057 = 263 даН/м |
8. Определение коэффициента неравномерности эластичности в пролете [1, стр. 86].
|
|
(66) |

По данным расчетов построим графики жесткости и эластичности контактной подвески (рис. 8).
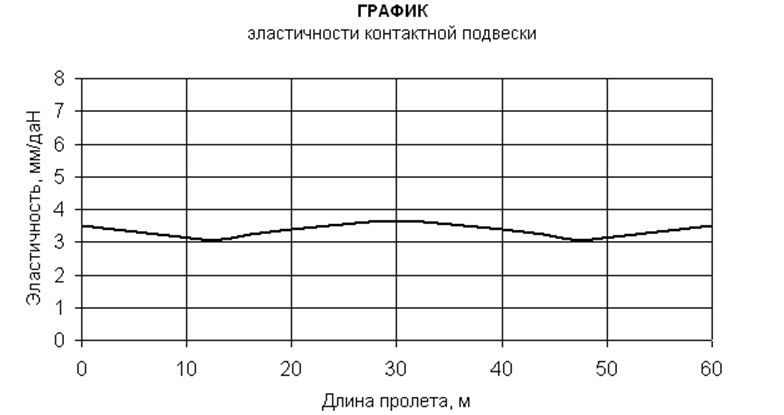 |
Рис. 8. Графики эластичности контактной подвески КС-200.
Литература
1. Фрайфельд А.В. Проектирование контактной сети. – 2 изд., перераб. и доп. Учебник для вузов ж. – д. транспорта. – М.: Транспорт, 1991. – 327 с.
2. Маркварадт К.Г. Контактная сеть. – 4-е изд., перераб. и доп. Учебник для вузов ж. – д. транспорта. – М.: Транспорт, 1994. – 335 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.