Перспективные контактные подвески: Методические указания к практическим занятиям, страница 4

G'_ф – часть нагрузки от веса фиксатора, передающаяся на контактный провод при воздействии токоприемника, даН;

n_к, n_c, n_ф – число соответственно контактных проводов, струн и фиксаторов;

Т, К, Н – натяжения соответственно несущего троса, контактного провода и троса рессорной струны, даН

Обозначения остальных величин приведены на рис. 1.

Если нажатие токоприемника Р приложено под струной, то для дальнейших расчетов можно воспользоваться выражениями, приведенными в таблице 1 (см. рис. 1).

Таблица 1

Если нажатие токоприемника Р приложено в середине между струнами, то для дальнейших расчетов можно воспользоваться выражениями, приведенными в таблице 2 (см. рис. 1).

Таблица 2

Силы, при которых происходит разгрузка различных струн, определяют по формулам, полученным на основании экспериментальных исследований:

В формулах (3), (4), (5), (6)

Остальные формулы [1] для определения подъемов контактных проводов в зонах А и Б получены с обычными допущениями – не учитывается собственная жесткость проводов, натяжение несущего троса и контактных проводов при нажатии токоприемника считаются неизменными. Кроме того, не учитываются подъемы контактных проводов и изменения натяжений рессорных тросов на опорах, соседних стой, для которой рассчитывается опорный узел. Однако введение в эти формулы опытных коэффициентов компенсирует допущения, принятые при выводе, и результаты расчетов по ним весьма близки к экспериментальным данным [1].

Для определения подъема контактного провода в точке 0 (рис. 1), если нажатие токоприемника не вызывает разгрузки подрессорных струн, можно составить расчетную схему (рис. 2).

На рис. 2 половина силы нажатия токоприемника Р отнесена к рассматриваемому пролету, а вторая половина – к соседнему (левому) пролету. Определив сумму моментов всех сил относительно точки Б сначала до, а затем после воздействия токоприемника, а после этого вычитая первую сумму из второй, получим следующее выражение:

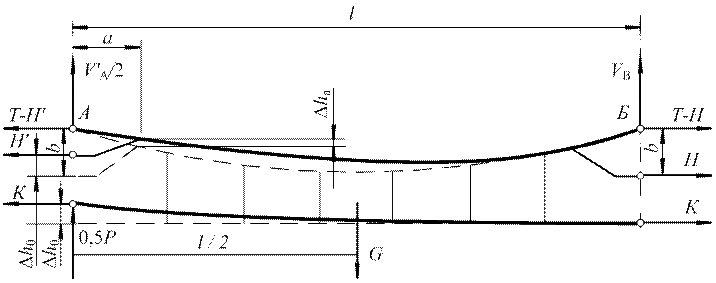
Рис. 2. Расчетная схема для определения ∆h₀

Пренебрегая незначительными горизонтальными перемещениями, рассмотрим уравнение равновесия сил в узле А до и после воздействия токоприемника (рис. 3).

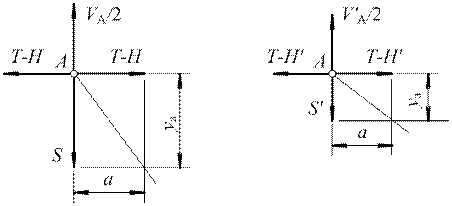
Рис. 3. Расчетные схемы для вывода уравнения равновесия в узле А

Вычитая первое уравнение для половины вертикальной составляющей опорной реакции из второго, получим

Подставим значение полуразности вертикальной составляющей опорной реакции из выражения (17) в выражение (16), выполним необходимые преобразования и найдем ∆h₀ (18).

Обозначим отношение подъемов проводов ∆h_а / ∆h₀ = γ₁ и подставим в выражение (18).