Перспективные контактные подвески: Методические указания к практическим занятиям, страница 5

Для определения подъема контактного провода в точке 1 (рис. 1), если нажатие токоприемника не вызывает разгрузки данной струны, составим расчетную схему (рис. 4).

Вызванное нажатием токоприемника изменение момента от вертикальных сил

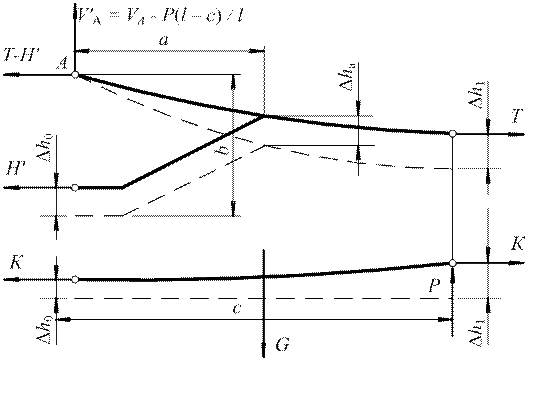
Рис. 4. Расчетная схема для определения величины ∆h₁

 

∆Мверт = Р(l – с)с / l,

(20)

а изменение момента от горизонтальных сил

∆Мгор = Т∆h1 + К(∆h1 – ∆h0) – Н'∆h0 + (Н' – Н)b

(21)

Приравняем выражение (20) к выражению (21) и выполним преобразования.

(22)

Обозначим отношение подъемов проводов ∆h₀ / ∆h₁ = γ₃, получим

(23)

Определение подъемов контактных проводов в основных точках пролета может быть выполнено по формулам, приведенным в таблице 3. Для зон А и Б (табл. 3) формулы даны без учета влияния изменений натяжения рессорного троса. Формулы для зоны В (табл. 3) составлены по работам    И.И. Власова и Ю.И. Горошкова. Также в таблице 3 указаны эмпирические формулы для вычисления опытных коэффициентов  γ.

У контактных подвесок с одним и двумя контактными проводами при совмещенных струнах, по экспериментальным данным, подъемы проводов в точках 01 и 50 (рис. 1) до разгрузки соседних струн на 10%, а после разгрузки соседних струн на 25% выше, чем в точках 0 и 0'. В точках 12 и 45 до разгрузки соседних струн подъемы проводов на 35%, а после разгрузки соседних струн на 65% выше, чем в точках 1 и 5. У контактных подвесок с двумя контактными проводами и шахматным расположением струн в точках 01, 50, 12 и 45 будут находиться струны. Подъемы проводов в точках 01 и 50 будут примерно такими же, как в точках 0 и 0', а в точках 12 и 45 – на 10% выше, чем в точках 1 и 5.

При расчетах подвесок с шахматным расположением струн, расстояния с и с₁ в соответствующих формулах нужно принимать по тому из контактных проводов, у которого подрессорная струна ближе к опоре, а расстояния с учитывать по несущему тросу.

Для практических расчетов можно принять, что жесткость контактной подвески вдоль пролета распределяется по кривой (рис. 5). Для построения этой кривой необходимо определить только жесткости подвески в точках 0 и

Таблица 3

Расчетные зоны и точки (рис. 1)	Расчетные формулы при условиях
	до разгрузки данной струны		после разгрузки данной струны, но до разгрузки соседних струн		после разгрузки соседних струн
А (0 и 0')		(24)		(25)	–
		(26)		(27)
Б (1 и 5)		(28)		(29)		(30)
	γ3 = a(1 – 0,05a) / c	(31)	γ4 = 1 + a / (P – R1)	(32)		(33)
В (2, 3, 4)		(34)		(35)		(36)
В (23, 34)	–			(37)	, где ∆h'c определено при Р = 2Rс	(38)

1 и в середине пролета (рис. 1). Закон изменения жесткости между точками 0 и 1 (5 и 0) может быть принят линейным, а между точками 1 и 5 параболическим. При этом на участках между точками 0 и 1 (5 и 0) допустимо принимать жесткость контактной подвески равной среднему их двух значений для этих точек, а жесткость в середине пролета, если неизвестно, будет ли в этом месте струна, – среднему из значений при наличии и отсутствии струны. Как показали сравнительные расчеты, такие упрощения незначительно отражаются на конечных результатах.

Таким образом, при 0 ≤ x ≤ c  и  l – c ≤ x ≤ l  имеем ж_кх = ж'_к0,                 а при  c ≤ x ≤ l – c

(39)

Последовательность решения задачи по расчету эластичности и жесткости контактной подвески

Студенты выполняют практическую работу по двум вариантам. Первый вариант соответствует нечетным номерам, а второй вариант – четным номерам по списку студентов в учебном журнале. Первому варианту предлагается выполнить расчет эластичности контактной подвески КС-160, а второму варианту – КС-200.