До выполнения расчетов эластичности (жесткости) контактной подвески студенты должны составить список исходных данных, в котором необходимо привести силовые и геометрические параметры контактных подвесок в соответствии со своим вариантом, марку применяемых проводов и тросов, а также силу расчетного нажатия токоприемника. Далее, на основании приведенных геометрических параметров контактных подвесок, студенты должны вычертить в масштабе расчетную схему (половины пролета) соответствующих контактных подвесок.
При проведении расчетов эластичности (жесткости) контактных подвесок по вышеприведенной методике, студенты кратко должны пояснять суть тех или иных будущих расчетов, а также резюмировать итоги этих расчетов.
После проведения расчетов эластичности (жесткости) контактных подвесок по итогам этих расчетов студентам необходимо рассчитать коэффициент неравномерности эластичности в пролете и построить графики зависимости эластичности (жесткости) контактных подвесок.
По итогам расчетов студенты должны дать краткие выводы, в которых должны быть предложены меры по выравниванию эластичности в пролете и по повышению эластичности на заданном участке.
Примеры выполнения расчетов эластичности и жесткости контактных подвесок КС-160 и КС-200 приведены ниже.
Задача 1
Построить
кривые жесткости и эластичности и определить коэффициент неравномерности эластичности
в пролете длиной 65 м компенсированной рессорной подвески М-95+НлФ-100 при
действительном нажатии токоприемника 15 даН. Рессорный трос выполнен из провода
М-35 с натяжением 350 даН.
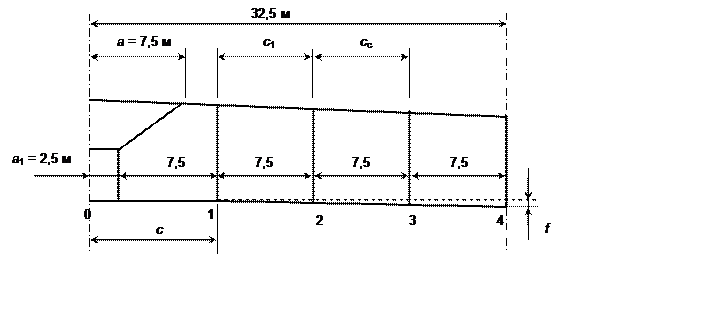
Рис. 5. Расчетная схема контактной подвески
Исходные данные:
а = 7,5 м; а1 = 2,5 м; с = 10 м; с1 = 7,5 м; сс = 7,5 м; l = 65 м ; К = 1200 даН; Т = 1420 даН; Н = 350 даН; nк = 1; gк = 0,873 даН/м; gр = 0,32 даН/м; nc = 2; nф = 1; G'c =0,3 даН; G'ф = 1,7 даН; P = 15 даН.
1. Определение стрелы провеса контактного провода [1, стр. 92]
|
|
(40) |
|
где f – стрела провеса контактного провода, м. |
f = (65 – 2 · 10) / 1000 = 0,045 м
2. Определение подъема контактного провода в точке 0.
Сравним расчетные нажатия токоприемника N [1, стр. 82] с силой R0 [1, стр. 82], при которой начинается разгрузка подрессорных струн.
|
|
(41) |
N = 4 · 0,045 · 1200 / (65 – 2 · 10) = 4,8 даН
|
Ro = nк gк (с + a1) + gp · 2a + ncG'c + nфG'ф + 2N |
(42) |
|
где nк – число контактных проводов; gк – нагрузка от веса контактного провода, даН/м; с – расстояние от точки подвеса несущего троса до околоопорной струны, м; a1 – расстояние от точки подвеса несущего троса до подрессорной струны, м; gp – нагрузка от веса рессорного троса, даН/м; a – расстояние от точки подвеса несущего троса до точки крепления рессорного троса на несущем тросе, м; nc – число струн; G'c – нагрузка от веса струнового зажима и части струны, даН; nф – число фиксаторов; G'ф – нагрузка от веса фиксатора, даН. |
|
R0 = 1 · 0,873 · (10 + 2,5) + 0,32 · 2 · 7,5 + 2 · 0,3 + 1 · 1,7 + 2 · 4,8 = 27,61 даН
Так как R0 > N и R0 больше действительного нажатия токоприемника P, то разгрузки подрессорных струн не произойдет. Подъем контактного провода ∆h0 определим по выражению [1, стр. 85, ф.148], м
|
|
(43) |
Значение коэффициента γ1 определим по выражению [1, стр. 85, ф.150]
|
|
(44) |
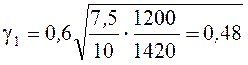
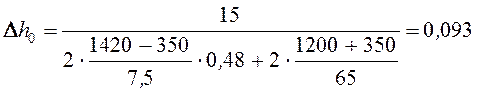м
3. Определение эластичности э0, мм/даН, и жесткости ж0, даН/м, в точке 0.
эо = ∆h0 / Р = 93 / 15 = 6,2 мм/даН
ж0 = Р / ∆h0 = 15 / 0,093 = 161 даН/м
4. Определение подъема контактного провода в точке 1.
Сравним расчетное нажатие токоприемника N1 с силой R1, при которой начинается разгрузка околоопорной струны, и расчетное нажатие токоприемник N'1 с силой R'1, при которой начинается разгрузка соседних с этой точкой струн.
Значение N1, даН, определим по выражению [1, стр. 82, ф.143]
|
|
(45) |
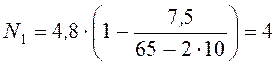даН
Значение N'1, даН, определим по выражению [1, стр. 82, ф.144]
|
|
(46) |
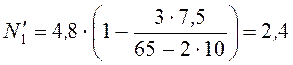даН
Значение R1, даН, определим по выражению [1, стр. 82, ф.139]
|
R1 = nкgк · 0,5(c – a1 + c1) + G'c + N1 |
(47) |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
