Перспективные контактные подвески: Методические указания к практическим занятиям, страница 7

R₁ = 1 · 0,873 · 0,5 · (10 – 2,5 + 7,5) + 0,3 + 4 = 10,85 даН

Значение R'₁, даН, определим по выражению [1, стр. 82, ф.140]

R'1 = nкgк · (c + 1,5c1) + 3G'c + N'1

(48)

R'₁ = 1 · 0,873 · (10 + 1,5 · 7,5) + 3 · 0,3 + 2,4 = 21,85 даН

Так R₁ < P, то околоопорные струны будут разгружены. Разгрузка соседних простых струн ввиду того, что R'₁ > P, не произойдет. Поэтому подъем контактного провода ∆h₁, м, определим по выражению [1, стр. 85, ф.153]

(49)

В последнем выражении

γ₃ = а(1 – 0,05а) / с = 7,5 · (1 – 0,05 · 7,5) / 10 = 0,47

γ₄ = 1 + а / (Р – R₁) = 1 + 7,5 / (15 – 10,85) = 2,81

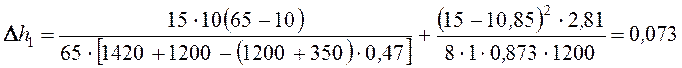 м

5. Определение эластичности э₁, мм/даН, и жесткости ж₁, даН/м, в точке 1.

э₁ = 73 / 15 = 4,87 мм/даН

ж₁ = 15 / 0,073 = 205 даН/м

6. Определение подъема контактного провода в точках 2, 3, 4.

Определение значения силы R_c, даН, при которой начинается разгрузка струн в этих точках [1, стр. 82, ф.141].

Rc = (nкgкcc + G'c – Nc)(T + К) / Т

(50)

Значение N_c, даН, в этом выражении найдем по формуле [1, стр. 82, ф.145]

Nc = 8fКcc / (l – 2c)2

(51)

N_c = 8 · 0,045 · 1200 · 7,5 / (65 – 2 · 10)² = 1,6 даН

R_c = (1 · 0,873 · 7,5 + 0,3– 1,6)(1420 + 1200) / 1420 = 9,68 даН        

Так как R_c > N_c и P > R_c, то струны в точках 2, 3 и 4 будут разгружаться. Ввиду того, что 3R_c > 15 даН, то подъем контактного провода, м, в указанных точках можно определить по следующему выражению [1, стр. 85, ф.159]

	(52)
где х – расстояние от точки подвешивания несущего троса до соответствующей струны, м.

Для струны в точке 2

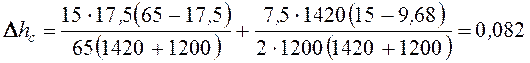м

Соответственно для струн в точках 3 и 4

∆hс3 = 0,097 м

∆hс4 = 0,102 м

7. Определение эластичностей и жесткостей в пролете в точках 2, 3, и 4.

э2 = 82 / 15 = 5,47 мм/даН ж2 = 15 / 0,082 = 183 даН/м	э3 = 97 / 15 = 6,47 мм/даН ж3 = 15 / 0,097 = 155 даН/м
э4 = 102 / 15 = 6,8 мм/даН ж4 = 15 / 0,102 = 147 даН/м

8. Определение коэффициента неравномерности эластичности в пролете [1, стр. 86].

(53)

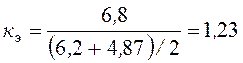
По данным расчетов построим графики жесткости и эластичности контактной подвески (рис. 6).

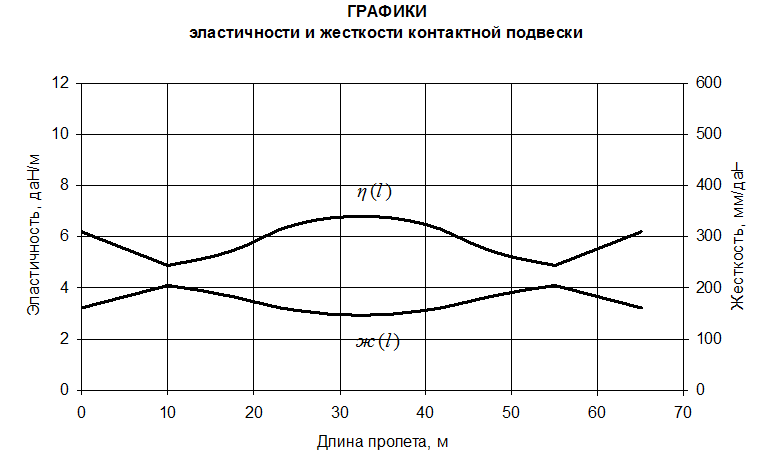
Рис. 6. Графики эластичности и жесткости контактной подвески КС-160.

Задача 2

Построить кривые жесткости и эластичности и определить коэффициент неравномерности эластичности в пролете длиной 60 м компенсированной рессорной подвески М-120+2МФ-120 при действительном нажатии токоприемника 15 даН. Рессорный трос выполнен из провода М-35 с натяжением 350 даН. Простые струны выполнены из провода МГ-16.

 

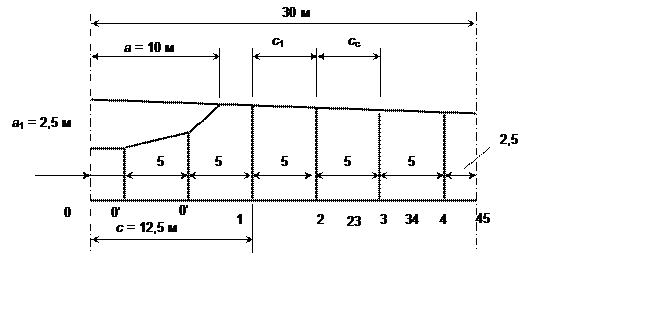Рис. 7. Расчетная схема контактной подвески

Исходные данные:

а = 10 м; а₁ = 2,5 м; с = 12,5 м; с₁ = 5 м; с_с = 5 м; l = 60 м; К = 1200 даН; Т = 1800 даН; Н = 350 даН; n_к = 2; g_к = 1,05 даН/м; g_р = 0,32 даН/м; n_c = 4; n_ф = 2; G'_c = 0,3 даН; G'_ф = 1,7 даН; P = 15 даН.

1. Определение стрелы провеса контактного провода.

Контактная подвеска КС-200 монтируется с беспровесным положением контактного провода.

f = 0 м.

2. Определение подъема контактного провода в точке 0 и 0'.

Сравним расчетные нажатия токоприемника N, даН, [1, стр. 82]с силой R₀, даН, [1, стр. 82] при которой начинается разгрузка подрессорных струн.

(54)

N = 4 · 0 · 2400 / (60 – 2 * 12,5) = 0 даН

R₀ = n_кg_к(с + a₁) + g_p · 2a + n_cG'_c + n_фG'_ф + 2N,

где n_к – число контактных проводов; g_к – нагрузка от веса контактного провода, даН/м; с – расстояние от точки подвеса несущего троса до околоопорной струны, м; a₁ – расстояние от точки подвеса несущего троса до подрессорной струны, м; g_p – нагрузка от веса рессорного троса, даН/м; a – расстояние от  точки  подвеса  несущего  троса  до точки крепления рессорного троса на несущем тросе, м; n_c – число струн; G'_c – нагрузка от веса струнового зажима и части струны, даН; n_ф – число фиксаторов; G'_ф – нагрузка от веса фиксатора, даН.

R₀ = 2 · 1,05 · ( 12,5 + 2,5 ) + 0,32 · 2 · 10 + 4 · 0,3 + 2 · 1,7 + 2 · 0   = 42,5 даН