Примеры решения задач по темам части № 1 «Строение и свойства твёрдых тел. Квантовые статистики»

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ПО ТЕМАМ ЧАСТИ №1

«СТРОЕНИЕ И СВОЙСТВА ТВЁРДЫХ ТЕЛ. КВАНТОВЫЕ СТАТИСТИКИ»

 Тема 1. Строение стёрдых тел

Основные формулы

1. Объем элементарной ячейки в кристаллах:

     а) кубической сингонии

                                                     ,

     б) гексагональной сингонии

                                                    ,

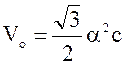где  и с  - параметры решетки.

2.  Период решетки (расстояние между ближайшими одноименными ионами)

      а) объемоцентрированной

                                               ,

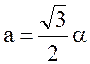      б) гранецентрированной

                                                    .

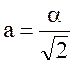3.  Объем одного моля кристалла

                                                 ,

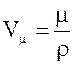где m - масса моля кристалла, r - его плотность.

4.  Число элементарных ячеек в одном моле кристалла

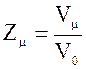                         или                        ,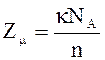

где k -одинаковое число атомов в химической формуле соединения, N_A - число Авогадро, n - число одинаковых атомов, приходящихся на элементарную ячейку.

5.  Число элементарных ячеек в единице объема кристалла

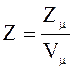                     или в общем случае      .

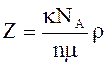В качестве индексов узлов кристаллической решетки принимается совокупность величин Х/а, У/в, Z/с, обозначаемых [[m n p]].

6.  Индексы направления в кристаллической решетке определяются наименьшими числами m, n, p, пропорциональными индексам любого узла, через который проходит прямая:

                                       m : n : p = Х/а : У/в : Z/с.

Индексы направления заключаются в одинарные скобки [m n p ].

7.  Миллеровские индексы плоскости задаются с помощью наименьших чисел h, k, l, обратных отрезкам u, v, w, отсекаемых плоскостью на координатных осях. Индексы плоскости записываются в круглых скобках (hkl).

9. Уравнение Вульфа-Брэггов для дифракции рентгеновского излучения на кристаллах имеет вид:

                                                ,

где d - межплоскостное расстояние, Q - угол скольжения, k - порядок дифракционного максимума.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1 .Сколько атомов приходится на одну элементарную ячейку объемоцентрированной кубической решетки?

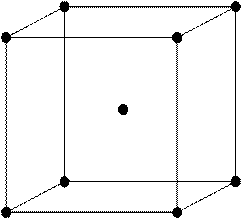                                                 Рис. 1

Решение:

Элементарная ячейка объемоцентрированной кубической решетки изображена на рис. 1. В этой ячейке имеются узлы кристаллической решетки двух типов: узлы, находящиеся в вершинах куба, и узел, находящийся на пересечении двух пространственных диагоналей куба. Каждый узел в вершинах принадлежит одновременно восьми элементарным ячейкам. Следовательно, на данную элементарную ячейку приходится 1/8 узла. Находящийся на пересечении диагоналей узел целиком находится в ячейке. Так как вершин восемь, то на одну элементарную ячейку в объемоцентрированной решетке приходится всего атомов

                                                   .

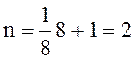Задача 2. Определить плотность кристалла стронция, если известно, что он имеет кристаллическую решетку гранецентрированной кубической сингонии, а период решетки d = 0,43 нм.

Дано: d = 0,43 нм, А = 87,6 кг/катом. Определить r.

Решение: Плотность кристалла стронция можно определить по формуле

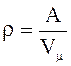                                                     .                                                (1)

Выразим объем одного моля кристалла V_m через объем элементарной ячейки V₀, воспользовавшись соотношением

                                                         V_m = V₀ Zm.

Но Z_m = N_A/n, а V₀ = a³, где а - параметр решетки. Для гранецентрированной ячейки

                     а = Ö2 d                  и              V₀ = 2Ö2 d³.

На гранецентрированную ячейку приходится  n = 4 атома. После подстановки указанных выше соотношений в формулу (1) окончательно для плотности кристалла получим выражение

                                            .

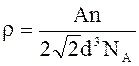Подставим числовые значения:

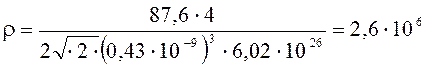                       кг/ м³.

Задача 3. На грань кристалла каменной соли падает параллельный пучок рентгеновских лучей с длиной волны 0, 147 нм. Определить расстояние меэду атомными плоскостями кристалла, если дифракционный максимум второго  порядка наблюдается, когда лучи падают на кристалл под углом 31⁰30^/.

Дано: l= 0,147 нм = 1,47 10^{-10 м;}  j = 31⁰30^/ ; k = 2. Определить d.

Решение: Запишем уравнение Вульфа-Брэггов

                                                     .

Угол q является дополнительным к углу j.

                                                   q= p/2 - j = 58⁰30^/.

Межплоскостное расстояние d определим из выражения

                                                      .

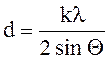Подставим числовые значения:

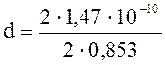                              = 1,7 10^-10 м = 0,17 нм.

Тема 2. Тепловые свойства твердых тел

Основные формулы

     1. Теплоемкость одного моля химически простых твердых тел определяется по закону Дюлонга и Пти

                                                     ,

где R - универсальная газовая постоянная.

2.  Теплоемкость одного моля химически сложных тел определяется по закону Неймана - Коппа

                                                             ,

где n - общее число частиц в химической формуле.

3.  Среднее значение квантового осциллятора, приходящаяся на одну степень свободы, в квантовой теории Эйнштейна:

                                    ,

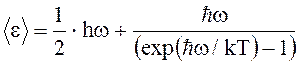где  - нулевая энергия,  - перечеркнутая постоянная Планка, w - циклическая частота,  k - постоянная Больцмана, Т - абсолютная температура.

4.  Внутренняя энергия одного моля кристалла в квантовой теории теплоемкости Эйнштейна