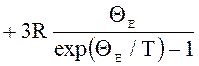Примеры решения задач по темам части № 1 «Строение и свойства твёрдых тел. Квантовые статистики», страница 2

                                   ,

где  - нулевая энергия одного моля кристалла,  - характеристическая температура Эйнштейна.

5.  Теплоемкость одного моля кристалла в квантовой теории теплоемкости Эйнштейна

                                  .

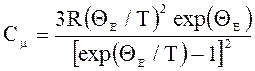При низких температурах  (<<)

                                  .

6.  Энергия одного моля кристалла по Дебаю

                             ,

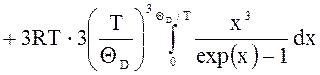
где  - нулевая энергия одного моля кристалла по Дебаю, - характеристическая температура Дебая, w_МАХ - максимальная частота, ограничивающая спектр колебаний.

7.  Теплоемкость одного моля кристалла по Дебаю

                 .

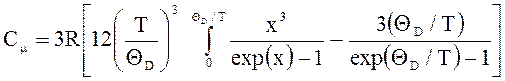При низких температурах  (Т<<)

                                           .

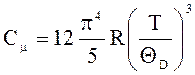8.  Энергия  фонона                 ,

где w - циклическая частота колебаний классической волны.

 9. Квазиимпульс фонона    ,

где l - длина волны, k - волновое число.

9.  Скорость фотона без учета дисперсии волны

                                              .

10.Среднее значение скорости звука в твердом теле

                                           ,

где V_t - cкорость поперечной звуковой волны, V_L - скорость продольной звуковой волны.

11.Коэффициент теплопроводности твердого тела

                                              ,

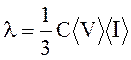где С - теплоемкость кристалла, рассчитанная на единицу объема, <I> - средняя длина свободного пробега фононов.

12.Линейный коэффициент теплового расширения

                                       a = gk / b² r₀ ,

где k - постоянная Больцмана.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1. Вычислить теплоемкость единицы объема кристалла бромистого алюминия AlBr₃ по классической теории теплоемкости. Определить количество теплоты необходимой для нагревания кристалла массой 10 г на 5 К.

Дано: m =10 г = 10^{-2 кг,}  DТ = 5 К. Найти С и DQ.

Решение: Теплоемкость единицы объема кристалла можно определить по формуле

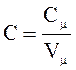                                                   ,                                                             (1)

где С_m  и V_m - теплоемкость и объем одного моля вещества.

     По закону Неймана-Коппа

                                                   .                                                         (2)

Для кристалла бромистого алюминия n = 4.

Объем V_m  можно выразить через плотность кристалла: .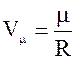

Масса одного моля AlBr₃: .

После подстановки всех вышенаписанных формул в (1) получим окончательное выражение для расчета теплоемкости.

                                               .

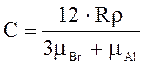Из таблиц физических величин имеем r = 3,01 10³ кг/м³, m_Br = 80 10^-3 кг/ моль, m_Аl = 27 10^-3 кг/моль. С учетом этих данных рассчитаем значение теплоемкости.

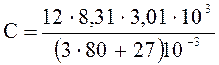                       = 1,12 10⁶ Дж/ (м³К) = 1,12 МДж /(м³К).

      Количество тепла, необходимое для нагревания кристалла от Т₁  до Т₂, можно определить по формуле

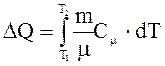                                            .                                                      (3)

      Теплоемкость С_m по классической теории от температуры не зависит ( см. формулу (2)), поэтому выражение (3) можно переписать в виде

                                               .

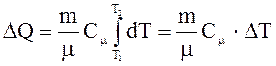     Подставим числовые значения и учтем, что С_m = 12 R:

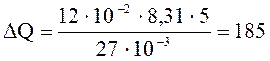                                               Дж.

Задача 2. Пользуясь теорией теплоемкости Эйнштейна, определить изменение внутренней энергии одного моля кристалла при нагревании его от 0 до 0,1Q_Е. Характеристическая температура для данного кристалла равна 300 К.

Дано: Т₁ = 0, Т₂ = 0,1 Q_Е, Q_Е = 300 К. Найти D_m.

Решение: Внутренняя энергия одного моля кристалла в квантовой теории теплоемкости Эйнштейна может быть определена по формуле

                                    .

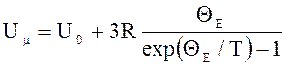Изменение внутренней энергии