Примеры решения задач по темам части № 1 «Строение и свойства твёрдых тел. Квантовые статистики», страница 4

Частоту w можно выразить через скорость фонона и его волновое число, воспользовавшись формулой

                                                          .

Из вышенаписанных формул энергия фонона определится как

                                                         .

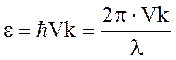Энергия будет максимальной при минимально возможном значении l. Для одномерной атомной цепочки l_min = 2a. C учетом последнего замечания формула для энергии фонона принимает вид:

                                                          .

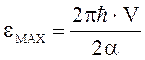Подставим числовые значения:

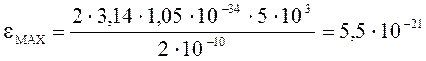                                  Дж.

Тема 3. Квантовые статистики

Основные формулы

     1. Плотность разрешенных квантовых состояний электронов внутри энергетической зоны

                                             ,

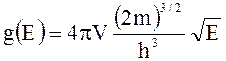где V - объем кристалла, m - масса электрона, Е - энергия электрона, h - постоянная Планка.

     2. Распределение Ферми  по энергиям для свободных электронов в металле

                                             ,

где

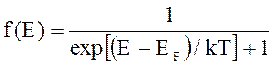                                              - функция распределения Ферми - Дирака.  Здесь Е_F - энергия Ферми, k - постоянная Больцмана.

 При Т = 0

                                                        f(E) = 1, если Е<Е_F;

                                                        f(E) = 0, если Е>Е_F.

     3. Температура вырождения электронного газа

                                                      .

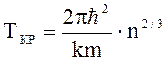     4. Температура Ферми электронного газа

                                                       ,

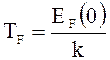где E_F(0) - энергия Ферми при Т = 0.

     5. Эффективная масса электрона в кристалле

                                                        ,

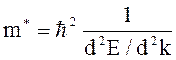где k - волновое число электрона.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1. Найти численное значение энергии Ферми для меди при температуре абсолютного нуля, учитывая, что на каждый атом меди приходится один свободный электрон  и что эффективная масса электрона приблизительно равна массе свободного электрона.

Дано: m = 63,5 10^-3 кг/моль; = 9, 1 10^-31 кг, r = 8900 кг/м³. Найти: Е_F (0) =?

Решение: Найдем связь концентрации электронов проводимости с энергией уровня Ферми. Общее количество электронов проводимости в металле может быть найдено по формуле

                                                 .

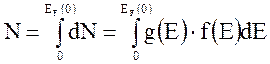После подстановки формул для функций g(E) и f(E) в выражение (1)

                        ,                ,

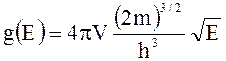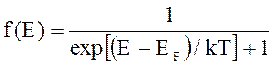учитывая, что n = N/V, получим для концентрации электронов

                                       .

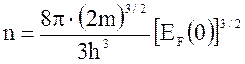Отсюда энергия Ферми

                                          .

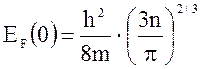По условию задачи концентрация свободных электронов в меди равна концентрации атомов меди, следовательно,

                                                         ,

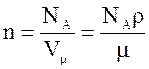где V_m - объем одного моля меди, N_A - число Авогадро.

Подставим числовые значения:

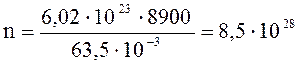                                        м^-3.

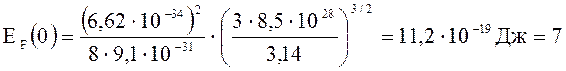                  эВ.

Задача 2. Вычислить среднее значение кинетической энергии электронов в меди при температуре абсолютного нуля, если энергия уровня Ферми равна 7 эВ.

Дано: Е_F = 7 эВ. Найти: <Е>.

Решение: Найдем суммарную кинетическую энергию всех электронов в металле, воспользовавшись формулой

                                 .

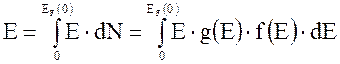Полное число электронов в металле

                                           .

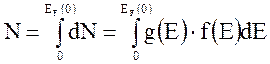Среднее значение кинетической энергии электронов

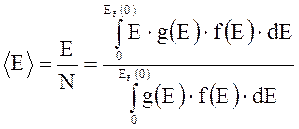                               .                                               (1)

После подстановки формул для функций g(E) и f(E) в выражение (1)

                        ,                

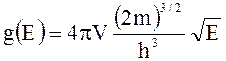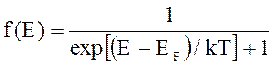
получим

                                             <Е> =.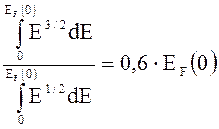

Подставим числовые значения:

                                            <Е> = 0,6 7 эВ = 4,2 эВ.