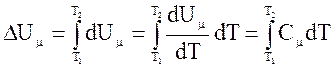Примеры решения задач по темам части № 1 «Строение и свойства твёрдых тел. Квантовые статистики», страница 3

                                    .                                 (1)

     Для низких температур (Т<< Q_Е) теплоемкость определяется по формуле

                                       .                                    (2)

Подставляя (2) в (1), получим

                                        .

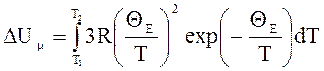     Введем новую переменную х = Q_Е / Т. Тогда 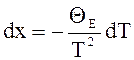. Температура Т₁ соответствует х₁ , стремящемуся в бесконечность, а температура Т₂  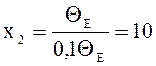- . Окончательно

                                         .

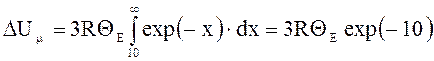     Подставим числовые значения:

                                        Дж.

Задача 3. Определить количество тепла, необходимое для нагревания кристалла каменной соли массой 10 г на 1 К. Характеристическая температура Дебая для NaCl  принять равной 320 К. Расчеты произвести для двух случаев:

1)  нагревание происходит от температуры Т₁ = Q_D;

2)   нагревание происходит от температуры Т₂ = 1 К.

Дано: m = 10г = 10^{-2 кг;} DТ = 1 К; Q_D = 320 К; Т₁ = Q_D; Т₂ = 1 К. Найти DQ₁ и DQ₂.

Решение: Количество теплоты DQ можно вычислить по формуле

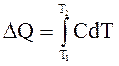                                                      .                                                      (1)           

Теплоемкость тела С связана с молярной теплоемкостью С_m соотношением

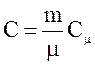                                                        .                                                        (2)

После подстановки  (2) в (1) имеем

                                                       .

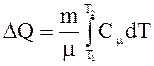     Теплоемкость С_m  в интервале температур DТ = 1 К можно считать независящей от температуры. С учетом этого

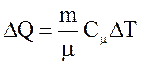                                                           .                                            (3)     

Теплоемкость одного моля в теории Дебая выражается формулой

                               .

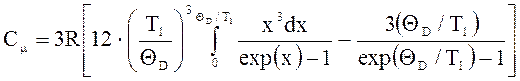При Т₁ = Q_D интеграл 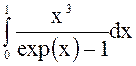= 0,225  (см. таблицы интегралов)и, следовательно,

                               .

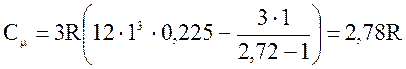Подставляя значение С_m в формулу (3), получаем

                                                    .

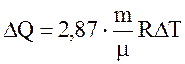Подставим числовые значения:

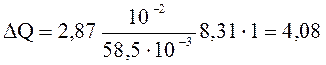                                             Дж.

     Во втором случае Т<<Q_D , поэтому можно использовать формулу Дебая в виде

                                                     .

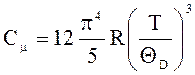После интегрирования

                                          .

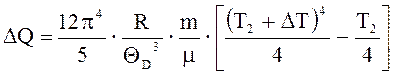С учетом значений Т₂ и DТ

                                            .

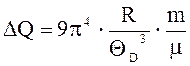Подставим числовые значения:

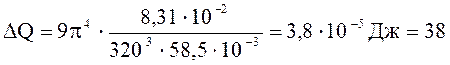                                   мкДж.

Задача 4. Определить величину квазиимпулься фонона, соответствующего частоте w = 0,1w_max. Усредненное значение скорости звука в кристалле <V> = 1380м/с. Характеристическая температура Дебая 100 К. Дисперсией звуковых волн в кристалле пренебречь.

Дано: w = 0,1w_max; <V> = 1380м/с; Q_D = 100 К. Найти: p -?

Решение: Импульс фонона может быть вычислен по формуле

                                                                   .

При отсутствии дисперсии звуковых волн волновое число определяется как

                                                                  ,

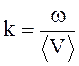следовательно, импульс фонона

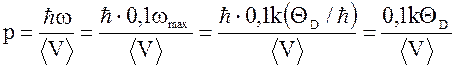                                     .      (1)

В выражении (1) учтено, что .

Подставим в (1) числовые значения:

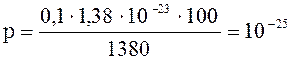                                      кг м/с.

Задача 5. Период решетки одномерного кристалла равен 0,3 нм. Атомы одномерного кристалла образуют не взаимодействующие друг с другом цепи. цепи. Определить максимальную энергию фононов, распространяющихся вдоль этой цепочки атомов. Скорость звука в кристалле принять равной 5 км/с.

Дано: а = 0,3 нм = 3 10^{-10 м;} V = 5 10³ м/с. Найти: e_max -?

Решение: Энергия фонона может быть найдена по формуле

                                                            .