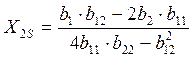Разработка математической модели технологического процесса с применением метода центральных композиционных ортогональных планов, страница 4

,

      Для определения расчетного значения параметра оптимизации, подставляют значения х_1S и x_2S в уравнение (12) и вычисляют y_S.

2) Два этапа преобразования уравнения (11) к каноническому виду (12) выполняется: при помощи параллельного переноса начала координат в точку S, при этом освобождаются от линейных членов, затем посредством поворота осей координат на некоторый угол α освобождаются от эффекта взаимодействия. Определение угла α по формуле:

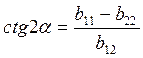,                                                 (19)

Из этого следует, что значения координат в каноническом и кодированном виде связаны следующими уравнениями:

х₁ =(Х₁ + х_1s)соsα-(Х₂ +х_2s)sinα;

                                                                                                                      (20)

х₂ =(Х₁ + х_1s)sinα + (Х₂ +х_2s)соsα.;                        

3) Для вычисления коэффициентов b₁₁ и b₂₂ составляем характеристический детерминант:

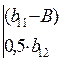
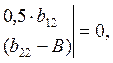                                                                                                                             (21)

 Расчет коэффициентов В₁₁ и В₂₂  производится по формуле:

,                                                                                                                        (22)

  Переменные В₁₁=х₁;  В₂₂=х₂  получаем при решении квадратного уравнения;

 Поверхность отклика определяется по знакам коэффициентов В_ii. Если коэффициенты  имеют одинаковые знаки, то  поверхность представляет собой элептический параболоид, если противоположные знаки – гиперболический параболоид.

В рассматривае­мом случае Вii имеют разные знаки, поэтому поверхность отклика имеет вид гиперболическо­го параболоида.

В результате исследования получаем вид поверхности, которая описывается уравнени­ем 2^го порядка.

Трудности геометрической интерпретации уравнения регрессии 2 порядка возрастают с увеличением количества факторов и при к>3 дать наглядное геометрическое представление поверхности невозможно.

Рассматривая изменения 2-ух факторов, застабилизировав остальные на каком-либо уровне в этом случае канонические преобразования дают хорошие результаты. Как правило, это центральный уровень. Не значимые факторы стабилизируют на нижнем уровне.

Ис­следование и оптимизацию технологического процесса ведут по двум факторам, которые наиболее сильно влияют на процесс, оставшиеся факторы стабилизируют на центральном уровне - их значение в кодированном виде равно 0.

Оптимизация технологического процесса

Оптимизация технологического процесса зависит от вида поверх­ности отклика. Применяем два метода для оптимизации технологического процесса: метод «Ридж-анализа» и метод движения вдоль канонических осей, так как в нашем случае поверхность имеет форму гиперболического параболоида. Метод «Ридж-анализа» основывается на методе неопределённых множителей Лагранжа. Для выбора оптимальных режимов составляют систему уравнений, в которой количество уравнений равно количеству коэффициентов уравнения регрессии:

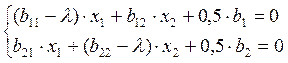,                                                                                                                        (23)

где λ – неопределенный множитель Лагранжа, который задается исследователем.

Формулы для вычисления Х₁ и Х₂ имеют следующий вид:

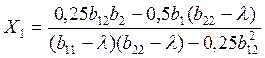
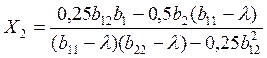                        (24)

 Исходными данными является уравнение регрессии в кодированном виде, подставляем значения Х₁ и Х₂, и вычисляем значение у (параметра оптимизации).

Если необходимо найти максимальный параметр оптимизации, λ выбирается больше максимального коэффициента канонического уравнения:

                                           ,                                           (24)

Если необходимо найти минимальный  параметр оптимизации, λ выбирается меньше минимального коэффициента канонического уравнения:

                                           у<,                                           (25)

Неопределенный множитель Ла−Гранджа лежит в интервале от max или min значений коэффициентов но, с другой стороны ограничивается параметром Хорля  (λ’), который вычисляется по формуле:

                                           ,                                           (26)

где b_kk – значение коэффициента в кодированном виде.