Разработка математической модели технологического процесса с применением метода центральных композиционных ортогональных планов, страница 2

1. Описание алгоритма расчёта

1.1 Обоснование выбора методов получения математической модели и оптимизации технологического процесса

Для наиболее точного описания области, близкой к экстремуму выбираю метод центральных ортогональных  композиционных планов второго порядка и получаем математическую модель. Данный выбранный метод имеет ряд следующих преимуществ:

           Для оптимизации технологического процесса были выбраны «Ридж-анализ» и метод движения вдоль канонических осей, т. к. они наиболее просты, обеспечивают высокую скорость движения к оптимуму и практически всегда приводят в точку оптимума.

Использован метод движения вдоль канонических осей, т. к. он позволяет получить два оптимальных режима в силу симметричности поверхности отклика и выбрать из них наиболее эффективный с точки зрения технологии.                

1.2. Математическая модель и формулы

 Построение матрицы  планирования  эксперимента центральных композиционных ортогональных планов производится по следующим правилам: за основу матрицы планирования эксперимента берут полный факторный эксперимент плана первого порядка. К точкам ПФЭ добавляют 2k-звездных точек, расположенных на расстоянии звездного плеча ±α, и в центре плана проводят один эксперимент n₀. Таким образом, получили матрицу с общим количеством опытов:

,

где n₀ - количество опытов в центре плана, согласно заданию принимаем n₀=1.

                                                                              (1)

где k−количество независимых факторов, в данном случае k=4<5, следовательно, ядро таких планов будут составлять планы пер­вого порядка ПФЭ (2^k).

Подставив значения в формулу, получим:

n=2⁴+2*4+1=25

Каждая строка – условие проведения одного эксперимента.

Заполнение ведется по столбцам: 1 столбец матрицы - это фиктивная переменная (x₀) всегда равна +1 (запол­няются все n строк); 2 столбец - равномерное чередование +1 и -1; 3 столбец - равномерное чередование 2^x +1 и 2^x -1; последующие столбцы заполняются по формуле 2^К-1, где к - коли­чество факторов. Столбцы взаимодействий получаем перемножением соответствующих столбцов X_i.

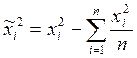      После исключения незначимых факторов, чтобы  не производить перерасчет коэффициентов уравнения регрессии, провожу ортогонализацию столбцов x_i² между собой за счет изменения количества параллельных опытов изменения в центре плана, следовательно, изменяется звездное плечо, и x₀ и x_i² путем преобразования квадратичных столбцов по формуле:

                                                  ,                                            (2)

Таким образом, с помощью указанных действий мы построили матрицу планирова­ния.

Регрессионный анализ

 Регрессионный  анализ состоит из основной задачи которая предусматривает  получению математической моде­ли процесса, проверке адекватности полученной модели и оценке влияния каждого фактора на процесс. Регрессионный анализ проводим по первой схеме.

1

1) Классический метод вычисления дисперсия  воспроизводимости состоит в   следующем. В любой точке плана проводим несколько параллельных опытов и по ним считаем выборочную дисперсию, которую затем и принимаем за дисперсию воспроизводимости. Чаще всего эти параллельные опыты проводят в центре плана.

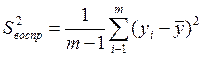                                  (3)

где m- количество параллельных опытов в матрице;

у_i - экспериментальные значения параметров оптимизации;