Методы регрессионного и корреляционного анализов: Учебно-методическое пособие по выполнению лабораторной работы, страница 6

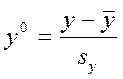
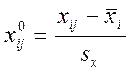
,                  ,                     (1.29)

где       х_ij⁰, у⁰-нормированные  значения соответствующих факторов и параметров оптимизации;

-математические ожидания соответствующих величин;

s_у,s_xi- среднеквадратичные отклонения переменных.

s_y=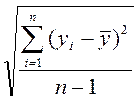,            s_xi=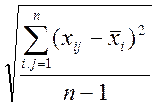,                (1.30)

2. Вычисление коэффициентов парной корреляции.

Для нормированных величин имеем:

,        ,       ,     

Поэтому выборочный коэффициент парной корреляции при этом вычисляют по формуле:

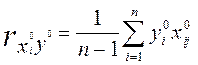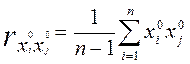,                 ,       (1.31)

Вычисленные по этой формуле  коэффициенты корреляции равны коэффициентам корреляции между переменными в натуральном виде.

3. Проверяют существенность влияния факторов на процесс и их закоррелированность методом парной корреляции ( см.  6.1)предыдущую тему ).

Незначимые и закоррелированные факторы из расчетов исключаются.

4. Уравнение регрессии получаем в нормированном виде , т.к. исходные данные переведены в нормированный вид . Это делается для упрощения расчетов.

Уравнение регрессии в нормированном виде не имеет  свободного члена в₀ и принимает вид:

у⁰=а₁х₁⁰+а₂х₂⁰+....+а_кх_к⁰,                                      (1.32)

Коэффициенты уравнения регрессии а_i находят методом наименьших квадратов .

Система нормальных уравнений имеет вид :

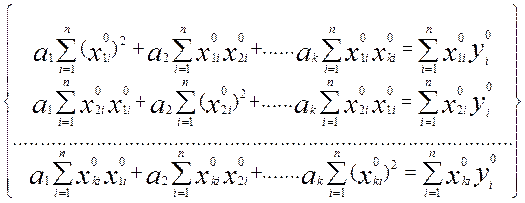,                (1.33)

Умножим левую и правую части системы уравнений на 1/(n-1). В результате при каждом коэффициенте а_i получается коэффициент парной корреляции.

Принимая во внимание, что

,

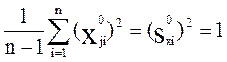получаем систему уравнений в виде:

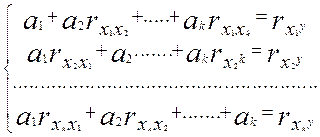                                     (1.34)

Решая полученную систему получаем коэффициенты уравнения регрессии в нормированном виде а_{i .}Перевод уравнения в натуральный вид производят по формулам:

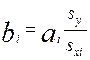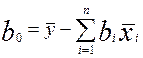,      ,                                            (1.35)

Математическая модель будет выражаться следующим уравнением:

y=b₀+b₁x₁+b₂x₂+....+b_kx_k,                                                   (1.36)

5. Вычисляют коэффициент множественной корреляции (R).

R=,                                          (1.37)

Коэффициент множественной корреляции показывает силу линейной стохастической связи между параметром у и множеством факторов х_i.

0<R<1

5.  Далее проводят регрессионный анализ по первой или второй схеме в зависимости от наличия параллельных опытов в экспериментах .

2 ЗАДАНИЯ НА ЛАБОРАТОРНУЮ РАБОТУ

Методы корреляционного анализа

Условие задачи. Методом множественной корреляции разработать оптимальную математическую модель процесса получения бутадиенстирольного каучука методом эмульсионной полимеризации. В качестве параметра оптимизации (У) принять выход каучука в %.

На процесс влияют следующие факторы:

Х₁ – температура процесса^{, 0}С;

Х₂ – давление, атм;

Х₃ – интенсивность перемешивания массы, об/мин;

Х₄ – количество эмульгатора, % от реакционной массы;

Х₅ – количество инициатора, % от реакционной массы.

В таблице 2.1 для каждого варианта задания указаны номера столбцов параметров оптимизации (У) и факторов (Х).

В таблице 2.2 приведены значения факторов (Х) и параметров оптимизации (У).

Исходными данными для каждого варианта будет матрица планирования эксперимента, состоящая из 6 столбцов и 15 строк.

В работе необходимо:

1) методом парной корреляции определить степень влияния факторов Х_i на технологический процесс и степень закоррелированности факторов между собой. Закоррелированные и не влияющие на процесс факторы из дальнейших расчетов исключить.

2) с применением программы множественного корреляционного анализа разработать три математических моделей процесса получения бутадиенстирольного каучука:

а) линейную

Y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ ……….+ b_nx_n;

б) показательную

Y = b₀ * b₁^x1 * b₂^x2 * b₃^x3 ………..*b_n^xn;

в) степенную

Y = b0 *x₁^b1 * x₂^b2 * x₃^b3…………*x_n^bn

3) проверить качество описания технологического процесса полученными математическими моделями;

4) рассчитать для каждой математической модели коэффициент множественной корреляции (R);