Методы регрессионного и корреляционного анализов: Учебно-методическое пособие по выполнению лабораторной работы, страница 2

Для того чтобы вычислить коэффициенты уравнения регрессии b_i существуют несколько способов. Наиболее простой и потому наиболее часто используемый на практике – метод наименьших квадратов.

1.1.3 Метод наименьших квадратов

В общем виде уравнение регрессии можно записать в виде:

y=f (x₁, x₂, x₃,..., x_k, b₀, b₁, b₂,..., b_к),                                 (1.4)

где       x₁, x₂,..., x_k – факторы, влияющие на процесс;

b₁, b₂,..., b_к – коэффициенты уравнения регрессии.

Задача состоит в том, чтобы по опытным данным определить значения b_i.Обычно условия всех опытов и их результаты представляют в виде таблицы (матрицы) и называют её матрица планирования экспериментов и результаты её реализации.

Таблица 1.1 – Матрица планирования экспериментов и результаты ее

реализации

Каждая строка матрицы – условия одного эксперимента. Каждый столбец – значения одного фактора в разных опытах; x_ij – значение i-ого фактора в j-ом опыте; x₀ – фиктивная переменная, равна +1.

Рассмотрим метод наименьших квадратов в наиболее обычном и простом варианте. Примем, что в опытах значения факторов х задавались с пренебрежимо малой ошибкой, значения отклика у получались со случайными ошибками.

В этом случае метод наименьших квадратов сводится к следующему: наилучшими будут те значения коэффициентов b_i, при которых сумма квадратов отклонений расчётных величин у от опытных у окажется наименьшей.

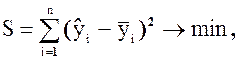                                                   (1.5)

то есть, те значения b_i, при которых сумма S окажется минимальной, являются наилучшими.

Как известно, для отыскания минимума функции нужно приравнять к нулю её частные производные по всем аргументам.

Таким образом, наилучшие b_i могут быть найдены как решение системы уравнений.

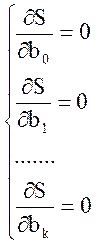,                                                                          (1.6)

В теории метода эти уравнения носят название нормальных уравнений.

Далее рассмотрим расчёт на примере однофакторной модели.

,                                                                     (1.7)

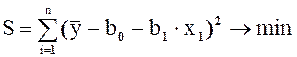,                                        (1.8)

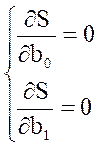,                                                                         (1.9)

Количество уравнений равно количеству коэффициентов b_i.

Для линейной зависимости после дифференцирования и алгебраических преобразований имеем следующую систему уравнений:

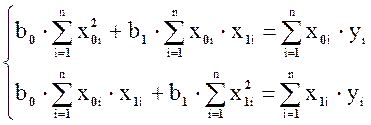,                            (1.10)

Решение системы при x_0i=1 даёт следующие формулы для вычисления коэффициентов b_i:

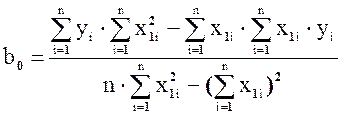,                                 (1.11)

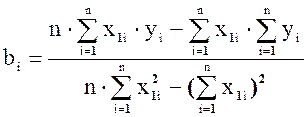,                                       (1.12)

Система нормальных уравнений (4.10) имеет интересные особенности:

а)  По диагонали левых частей системы под знаками суммы последовательно стоят квадраты независимых переменных;

б)  Относительно этой диагонали наблюдается симметрия;

в)  В правой части системы расположены произведения, полученные в результате последовательного умножения столбца параметра оптимизации на столбец факторов;

Эти особенности дали возможность найти простой метод составления системы нормальных уравнений для любого количества коэффициентов b_i:

а)  Первое уравнение системы получают умножением величин из столбца х₀ сначала на самого себя, а затем на все остальные x_i по очереди;

б)  Второе уравнение получают умножением величин из второго столбца х₁ на все остальные столбцы по очереди, начиная со столбца х₀;