Методы регрессионного и корреляционного анализов: Учебно-методическое пособие по выполнению лабораторной работы, страница 5

В химической технологии этот метод получения  математической модели не нашел широкого применения, т. к. практически не существует химико-технологических процессов , на которые бы влиял всего один фактор. В этом случае наибольший интерес представляет метод парной корреляции для оценки влияния факторов на процесс и степени закоррелированности факторов между собой. Это направление применения метода и рассмотрим подробнее.

При исследовании зависимости между факторами (х_i) и параметром оптимизации (у) необходимо убедиться в наличии связи между ними. Может оказаться , что связь между некоторыми факторами и параметром не существенна и тогда рассматривать зависимость между ними, т.е. разрабатывать математическую модель, не имеет смысла . Корреляционный анализ, как правило, является предварительной стадией моделирования  технологического процесса.

Существенность связи между х и у  в математической статистике определяют выявлением значимости (z) коэффициента парной корреляции (r_ху).

z=-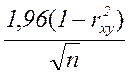,                                                                 (1.27)

     где          n- количество опытов.

Если z для данного r_ху больше нуля, то коэффициент r_ху -значим, т. е. значимо отличается от нуля. В этом случае связь между этим фактором х и параметром у существует , т.е. фактор х влияет на параметр у , а следовательно на технологический процесс. В противном случае коэффициент корреляции r_ху незначим, следовательно связь между х и у отсутствует, а фактор х не влияет на процесс и из дальнейших расчетов исключается.

Степень закоррелированности факторов между собой определяют аналогичным способом. Определяют значимость коэффициента парной корреляции между двумя факторами, например х₁ и х₂ , по формуле:

z=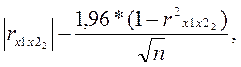                                                       (1.28)

Если z>0-коэффициент r_х1х2  значим , связь между факторами существует, т.е. факторы х₁ и х₂ закоррелированы.  В противном случае корреляция между факторами отсутствует, т.е. факторы не зависимы друг от друга. Присутствие закоррелированных  факторов  в математической модели недопустимо.

Поэтому, в случае закоррелированности, один из факторов следует исключить.

Какой из факторов следует исключить?

Исключают тот фактор, который в меньшей степени действует на процесс. Степень влияния на процесс определяют по значениям коэффициента корреляции между факторами х₁, х₂ и параметром оптимизации у , т.е. r_х1у и r_х2у. Большее значение коэффициента корреляции показывает большую тесноту линейной связи. Следовательно исключают тот фактор , для которого r_ху по абсолютной величине имеет меньшее значение.

Таким образом , метод парной корреляции  дает возможность выявить существенность и силу  влияния факторов на процесс. Закоррелированные и не влияющие на процесс  факторы из дальнейших расчетов исключаются.

1.2.2 Метод множественной корреляции

Метод множественной корреляции дает возможность получить многофакторную математическую модель технологического процесса.

В простейшем случае это уравнение регрессии первого порядка:

У = в₀ + в₁х₁ + в₂х₂ +....+ в_кх_к.,                                             (4.28)

Обычно исходными данными являются результаты “пассивного” эксперимента, которые представляют в виде матрицы.

Таблица 1.2  Матрица результатов экспериментов

Расчеты проводят в следующей последовательности:

1. Перевод исходных данных от натурального вида к нормированному по формулам: