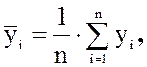Методы регрессионного и корреляционного анализов: Учебно-методическое пособие по выполнению лабораторной работы, страница 4

                                                                            (1.23)

2.  Рассчитывают дисперсию столбца y_i:

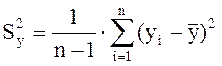,                                                            (1.24)

3.  Проверку значимости коэффициентов b_i аналогично первой схеме провести невозможно, так как отсутствует S²_воспр. Поэтому существенность влияния факторов определяют методом парной корреляции (раздел 1.2.1).

4.  Проверку адекватности уравнения регрессии произвести невозможно, так как отсутствует дисперсия воспроизводимости. В этом случае можно оценить качество аппроксимации принятым уравнением, сравнив остаточную дисперсию (S ² _ост) и выборочную дисперсию (S ² _y).

Вычисляют дисперсионное отношение (с):

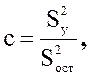                                                                            (1.25)

     где          S²_ост – остаточная дисперсия (S²_ост=S²_воспр+S²_ад).

S²_воспр отсутствует, поэтому S²_ост = S²_ад и вычисляется по формуле (1.22). Дисперсионное отношение (С) сравнивают с критерием Фишера. Если с>F_табл – качество описания процесса полученным уравнением хорошее, и чем больше значение с превышает F_табл, тем эффективнее уравнение регрессии. В этом случае критерий Фишера показывает, во сколько раз уменьшается рассеяние относительно полученного уравнения регрессии по сравнению с рассеянием относительно среднего ().

F_табл находят по степени свободы числителя f_ч=(n-1) и степени свободы знаменателя f_з=(n-L).

1.2 МЕТОДЫ КОРРЕЛЯЦИОННОГО АНАЛИЗА

1.2.1 Метод парной корреляции

Методы корреляционного, также как  и регрессионного анализа, широко применяются  для выявления и описания зависимости между случайными величинами по экспериментальным данным .

Для экспериментального изучения зависимости между величинами х и у

проводят некоторое количество независимых опытов. Результат  i-того опыта дает пару значений ( х_i ,у_i) , i=1,2....n. О наличии или отсутствии корреляции (зависимости) между двумя величинами качественно можно судить по полю корреляции,  нанеся точки (  х_i ,у_i)  на  координатную плоскость.

Для количественной оценки тесноты стохастической  линейной связи между двумя величинами служит выборочный коэффициент парной корреляции  (r_ху)

r_ху=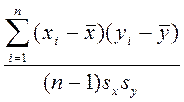,                                                     (1.26)

где       ху показывает величины , между которыми определяют тесноту связи;

-значения случайных величин х и у;

 -математические ожидания случайных величин х и у;

n- объем выборок х и у;

s_x, s_y -среднеквадратичные отклонения величин х и у.

Эта оценка является смещенной , но величина смещения убывает обратно пропорционально количеству  опытов (n) и при n>50  составляет менее 1%.

Поэтому на практике пользуются такой оценкой коэффициента парной корреляции.

Коэффициент парной корреляции по абсолютной величине не превосходит 1.

-1<r_xy<1

Крайние значения коэффициента корреляции  r_xy=1. Соответствуют линейной функциональной зависимости.

Коэффициент парной корреляции имеет следующее свойство: он не изменяется от прибавления к х и у каких-либо величин или от умножения х и у на положительные числа. Поэтому коэффициент парной корреляции не изменится, если от исходных случайных величин перейти к нормированным. Это свойство позволяет существенно упростить вычисления.

Методом парной корреляции можно получить однофакторную математическую модель технологического процесса вида у=в₀+в₁х₁  имея значения факторов (х _i) и соответствующие им экспериментальные значения параметра оптимизации. Коэффициенты уравнения в_i вычисляют методом наименьших квадратов, а затем проводят статистическую обработку результатов по первой или второй схеме регрессионного анализа в зависимости от наличия или отсутствия  параллельных  опытов в эксперименте.