Методы регрессионного и корреляционного анализов: Учебно-методическое пособие по выполнению лабораторной работы, страница 3

в)  Во всех уравнениях системы располагают коэффициенты b_i в одинаковом порядке по возрастанию индексов.

г) В правой части системы произведения столбца параметра у на соответствующий столбец x_i.

1.1.4 Схемы регрессионного анализа

После вычисления коэффициентов уравнения регрессии b_i приводят статистическую обработку результатов (регрессионный анализ).

В зависимости от наличия сведений о дисперсии воспроизводимости параметра оптимизации (S²_воспр) регрессионный анализ проводят по различным схемам.

Первая схема регрессионного анализа проводится при наличии параллельных опытов, то есть каждый эксперимент проводится не менее, чем два раза – опыты дублируются.

Первая схема регрессионного анализа проводится в следующем порядке:

1.  Вычисляют построчные (частные) математические ожидания (`y_i ):

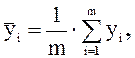                                                                            (1.13)

где     y_i – экспериментальные значения у параллельных опытов;

m – количество параллельных опытов.

2.  Вычисляют построчные дисперсии (S_i²):

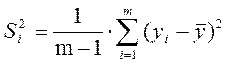,                                                                     (1.14)

3.  Проверяют однородность дисперсий:

При одинаковом количестве опытов по критерию Кохрена (G_р).

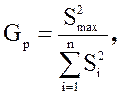                                                                              (1.15)

где     S_max² – максимальная построчная дисперсия;

n – количество опытов в матрице.

Полученное G_р сравнивают с табличным (G_табл). Если G_р< G_табл – дисперсии однородны и можно продолжить расчёт дальше. В противном случае дисперсии неоднородны и необходимо эксперимент, соответствующий максимальной дисперсии, провести более точно заново, а затем повторить проверку однородности дисперсий.

4.  Вычисляют общую дисперсию воспроизводимости (S²_воспр)

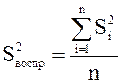,                                                                             (1.16)

при степени свободы f_воспр=(m-1)×n.

5.  Проверяют значимость коэффициентов уравнения регрессии по критерию Стьюдента (t_р):

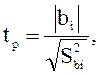                                                                                  (1.17)

     где          S_bi² – дисперсия коэффициента b_i.

Если t_р>t_табл при a=0,05 и f=f_воспр, то коэффициент b_i значимо отличается от нуля, то есть фактор, соответствующий этому коэффициенту оказывает существенное влияние на процесс. В противном случае коэффициент b_i незначим, фактор, соответствующий ему, влияния на процесс не оказывает и из уравнения исключается.

Дисперсия коэффициента b_i определяется по закону накопления ошибок:

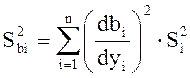,                                                                    (1.18)

Если выборочные дисперсии однородны, получим:

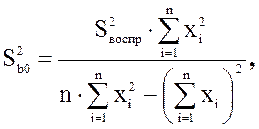                                                          (1.19)

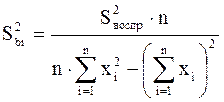,                                                     (1.20)

Оставшиеся, значимые коэффициенты b_i пересчитывают заново, поскольку матрица не ортогональна и коэффициенты b_i закоррелированы друг с другом.

6.  Проверяют адекватность уравнения регрессии.

Адекватность – соответствие полученной математической модели реальному процессу.

Проверку проводят по критерию Фишера (F_р).

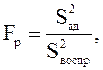                                                                          (1.21)

где  S_ад² – дисперсия адекватности.

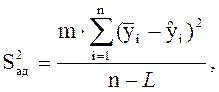                                                      (1.22)

где       – расчётный параметр оптимизации;

L– количество значимых коэффициентов b_i.

Полученный F_р сравнивают с F_табл. Если F_р<F_табл – уравнение адекватно. В противном случае уравнение неадекватно и следует перейти к планам более высокого порядка.

Критерий Фишера находят по таблицам по степеням свободы числителя (f_ч) и знаменателя (f_з).

f_ч=(n-L);

f_з=n×(m-1).

Вторая  схема регрессионного анализа применяется при отсутствии информации о дисперсии воспроизводимости, то есть отсутствии параллельных опытов, и проводится в следующем порядке:

1.  Рассчитывают математическое ожидание столбца y_i: