Системы диагностирования. Алгоритмы диагностирования и методы их построения, страница 9

Она делит множество состояний  на два подмножества  и . В табл. 2.3 и 2.4 приведены словари неисправностей для этих подмножеств, где указаны также значения , пересчитанные с учетом выражения (2.19). Для разделения множества  сначала применяется проверка , а затем – . Для разделения множества  проверки  и  используются в любой последовательности. Для полученного алгоритма (см. рис. 2.13) = 80, а следовательно, он лучше алгоритмов, приведенных на рис. 2.12.

                                  Т а б л и ц а   2.3                                               Т а б л и ц а   2.4

          При решении практических задач часто ОД может быть представлен в виде линейной цепи из последовательно включенных элементов (см. рис. 2.14).

Рис.2.14. Объект диагноза с последовательным включением

                  элементов

При отказе элемента на его выходе появляется недопустимый сигнал (отличный от сигнала на выходе исправного элемента), который вызывает возникновение недопустимого сигнала на выходе последующего элемента, а также всех других включенных за ним элементов. В цепи возможны отказы только одного элемента. Поэтому цепь из  элементов имеет  неисправных состояний , где  – состояние с неисправностью -го элемента. Проверка  заключается в измерении сигнала на выходе -го элемента. Измерения возможны на выходе каждого элемента.

          Рассмотрим два случая диагностирования системы из включенных последовательно элементов. В первом случае предполагается, что равны между собой вероятности отказов элементов,  также и стоимости всех проверок. Тогда оптимальным является алгоритм, который представлен на рис. 2.15, а для схемы рис. 2.14.

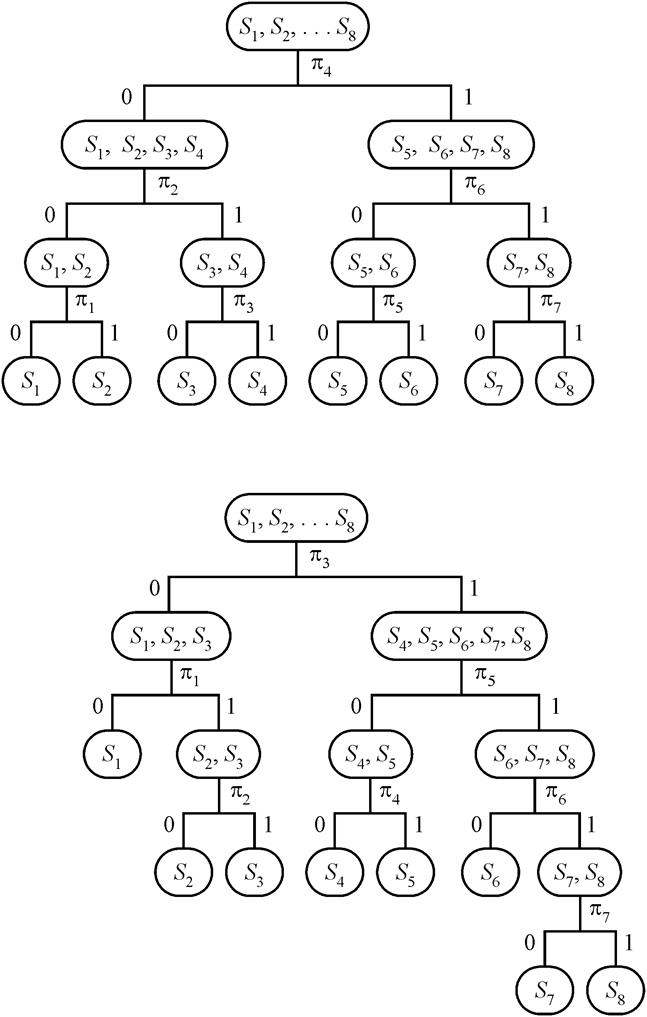
Рис.2.15. Алгоритмы диагностирования цепи из последовательно

                 включенных элементов

 Наибольшей информативностью обладает проверка, состоящая в измерении сигнала на выходе элемента с номером  (при четном числе элементов) или 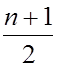 (при нечетном числе элементов), т.е. в измерении сигнала в середине цепи. При положительном результате проверки делается вывод, что неисправный элемент находится во второй половине цепи, а при отрицательном результате – что в первой половине цепи. Далее осуществляется измерение в середине той половины цепи, где находится неисправный элемент, и т.д. Последним будет произведено измерение выходного сигнала того элемента, на выходе которого присутствует недопустимый, а на входе – допустимый сигнал.

          Во втором случае предполагается, что равны между собой стоимости всех проверок, но вероятности отказов элементов отличаются друг от друга. Пусть, например, для системы рис. 2.14 имеем: = 0,2,  = 0,1. Для первой проверки выбирается элемент, выход которого делит цепь таким образом, что сумма вероятностей отказов элементов одной части цепи минимально отличается от такой же суммы для второй части цепи. В данном случае таким является третий элемент, так как = 0,5. Проверка  (см. рис. 2.15, б) делит цепь элементов на две неравные части, в первую из них входят элементы с номерами 1, 2 и 3, а во вторую – с номерами 4, 5, 6, 7 и 8. Выбор проверок для деления этих частей цепи на две части осуществляется по тому же правилу и т.д. В результате получаем алгоритм, представленный на рис. 2.15, б, при  построении которого учитывается энтропия системы. Предположим, что стоимость каждой проверки = 10. Тогда стоимость данного алгоритма = 40. При тех же условиях стоимость алгоритма, представленного на рис. 2.15, а, = 42. Она выше, так как при построении этого алгоритма не учитываются изменение энтропии системы при выборе проверок.

          Для построения алгоритмов с учетом как вероятности отказов элементов, так и стоимостей проверок применяется выбор проверок по максимальному отношению  .